Class 11-NCERT Solutions-Chapter-01-Sets -

CBSE Class 11
Mathematics
NCERT Solutions
Chapter-1-Sets

Which of the following are sets? Justify your answer.

The collection of all the months of a year beginning with the letter J.
The collection of ten most talented writers of India.
A team of eleven best-cricket batsmen of the world.
The collection of all boys in your class.
The collection of all natural numbers less than 100.
A collection of novels written by the writer Munshi Prem Chand.
The collection of all even integers.
The collection of questions in this Chapter.
A collection of most dangerous animals of the world.

▼

Answer:

A set is a well-defined collection of objects. "Well-defined" means we can definitely decide whether a given object belongs to the collection or not.

Yes, it is a set. The months are well-defined: {January, June, July}.
No, it is not a set. The criterion "most talented" is vague and varies from person to person.
No, it is not a set. The criterion "best" is subjective and not well-defined.
Yes, it is a set. It is possible to identify exactly who belongs to this collection.
Yes, it is a set. The numbers are {1, 2, 3, ..., 99}. This is well-defined.
Yes, it is a set. The books written by a specific author are fixed and well-defined.
Yes, it is a set. Even integers are mathematically defined.
Yes, it is a set. The questions in a specific chapter are countable and distinct.
No, it is not a set. "Most dangerous" is a subjective term.

Let \( A = \{1, 2, 3, 4, 5, 6\} \). Insert the appropriate symbol \( \in \) or \( \notin \) in the blank spaces:

5 . . . A
8 . . . A
0 . . . A
4 . . . A
2 . . . A
10 . . . A

▼

Answer:

The symbol \( \in \) stands for "belongs to" and \( \notin \) stands for "does not belong to".

\( 5 \in A \) (Since 5 is in set A)
\( 8 \notin A \) (Since 8 is not in set A)
\( 0 \notin A \) (Since 0 is not in set A)
\( 4 \in A \) (Since 4 is in set A)
\( 2 \in A \) (Since 2 is in set A)
\( 10 \notin A \) (Since 10 is not in set A)

Write the following sets in roster form:

\( A = \{x : x \text{ is an integer and } -3 \le x < 7\} \)
\( B = \{x : x \text{ is a natural number less than } 6\} \)
\( C = \{x : x \text{ is a two-digit natural number such that the sum of its digits is } 8\} \)
\( D = \{x : x \text{ is a prime number which is divisor of } 60\} \)
\( E = \text{The set of all letters in the word TRIGONOMETRY} \)
\( F = \text{The set of all letters in the word BETTER} \)

▼

Answer:

Integers between -3 (inclusive) and 7 (exclusive):
\( A = \{-3, -2, -1, 0, 1, 2, 3, 4, 5, 6\} \)
Natural numbers strictly less than 6:
\( B = \{1, 2, 3, 4, 5\} \)
Two-digit numbers summing to 8 (17, 26, 35, 44, 53, 62, 71, 80):
\( C = \{17, 26, 35, 44, 53, 62, 71, 80\} \)
Prime factors of 60 (Factors: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60. Primes: 2, 3, 5):
\( D = \{2, 3, 5\} \)
Letters in TRIGONOMETRY (repetitions removed):
\( E = \{T, R, I, G, O, N, M, E, Y\} \)
Letters in BETTER (repetitions removed):
\( F = \{B, E, T, R\} \)

Write the following sets in the set-builder form:

\( \{3, 6, 9, 12\} \)
\( \{2, 4, 8, 16, 32\} \)
\( \{5, 25, 125, 625\} \)
\( \{2, 4, 6, \dots\} \)
\( \{1, 4, 9, \dots, 100\} \)

▼

Answer:

These are multiples of 3 from 3 to 12.
\( \{x : x = 3n, n \in \mathbb{N} \text{ and } 1 \le n \le 4\} \)
These are powers of 2 (\(2^1\) to \(2^5\)).
\( \{x : x = 2^n, n \in \mathbb{N} \text{ and } 1 \le n \le 5\} \)
These are powers of 5 (\(5^1\) to \(5^4\)).
\( \{x : x = 5^n, n \in \mathbb{N} \text{ and } 1 \le n \le 4\} \)
These are all even natural numbers.
\( \{x : x \text{ is an even natural number}\} \)
These are squares of natural numbers from 1 to 10.
\( \{x : x = n^2, n \in \mathbb{N} \text{ and } 1 \le n \le 10\} \)

List all the elements of the following sets:

\( A = \{x : x \text{ is an odd natural number}\} \)
\( B = \{x : x \text{ is an integer}, -\frac{1}{2} < x < \frac{9}{2}\} \)
\( C = \{x : x \text{ is an integer}, x^2 \le 4\} \)
\( D = \{x : x \text{ is a letter in the word "LOYAL"}\} \)
\( E = \{x : x \text{ is a month of a year not having 31 days}\} \)
\( F = \{x : x \text{ is a consonant in the English alphabet which precedes } k\} \)

▼

Answer:

\( A = \{1, 3, 5, 7, \dots\} \)
Integers strictly between -0.5 and 4.5 are 0, 1, 2, 3, 4.
\( B = \{0, 1, 2, 3, 4\} \)
Integers whose square is \(\le 4\) are -2, -1, 0, 1, 2.
\( C = \{-2, -1, 0, 1, 2\} \)
Letters in LOYAL (L is repeated).
\( D = \{L, O, Y, A\} \)
Months with 30 or fewer days (excluding those with 31).
\( E = \{\text{February, April, June, September, November}\} \)
Consonants before 'k' (b, c, d, f, g, h, j).
\( F = \{b, c, d, f, g, h, j\} \)

Match each of the set on the left in the roster form with the same set on the right described in set-builder form:

(i) \( \{1, 2, 3, 6\} \)
(ii) \( \{2, 3\} \)
(iii) \( \{M,A,T,H,E,I,C,S\} \)
(iv) \( \{1, 3, 5, 7, 9\} \)

(a) \( \{x : x \text{ is a prime number and a divisor of } 6\} \)
(b) \( \{x : x \text{ is an odd natural number less than } 10\} \)
(c) \( \{x : x \text{ is natural number and divisor of } 6\} \)
(d) \( \{x : x \text{ is a letter of the word MATHEMATICS}\} \)

▼

Answer:

(i) matches (c): 1, 2, 3, 6 are all natural numbers and divisors of 6.
(ii) matches (a): 2 and 3 are the only prime numbers that divide 6.
(iii) matches (d): These are the distinct letters in the word MATHEMATICS.
(iv) matches (b): 1, 3, 5, 7, 9 are all odd natural numbers less than 10.

Correct Matches:
(i) \(\leftrightarrow\) (c)
(ii) \(\leftrightarrow\) (a)
(iii) \(\leftrightarrow\) (d)
(iv) \(\leftrightarrow\) (b)

Which of the following are examples of the null set?

Set of odd natural numbers divisible by 2
Set of even prime numbers
\( \{ x : x \text{ is a natural numbers}, x < 5 \text{ and } x > 7 \} \)
\( \{ y : y \text{ is a point common to any two parallel lines} \} \)

▼

Answer:

Null Set. No odd natural number is divisible by 2.
Not a Null Set. The set contains the element 2, which is an even prime number. \( \{2\} \ne \phi \).
Null Set. No natural number can be simultaneously less than 5 and greater than 7.
Null Set. Parallel lines never intersect, so they have no common point.

Which of the following sets are finite or infinite?

The set of months of a year
\( \{1, 2, 3, \dots\} \)
\( \{1, 2, 3, \dots, 99, 100\} \)
The set of positive integers greater than 100
The set of prime numbers less than 99

▼

Answer:

Finite. There are exactly 12 months in a year.
Infinite. The set of natural numbers goes on endlessly.
Finite. The set contains exactly 100 elements (natural numbers from 1 to 100).
Infinite. There are infinite integers greater than 100 (101, 102, 103, ...).
Finite. The prime numbers less than 99 are countable and limited.

State whether each of the following set is finite or infinite:

The set of lines which are parallel to the x-axis
The set of letters in the English alphabet
The set of numbers which are multiple of 5
The set of animals living on the earth
The set of circles passing through the origin (0,0)

▼

Answer:

Infinite. We can draw infinitely many lines parallel to the x-axis.
Finite. There are exactly 26 letters in the English alphabet.
Infinite. Multiples of 5 are \( 5, 10, 15, \dots \) which continue indefinitely.
Finite. Although the number is very large, it is a specific, countable number at any given time.
Infinite. Infinitely many circles can be drawn passing through a single point like the origin.

In the following, state whether \( A = B \) or not:

\( A = \{ a, b, c, d \} \quad B = \{ d, c, b, a \} \)
\( A = \{ 4, 8, 12, 16 \} \quad B = \{ 8, 4, 16, 18 \} \)
\( A = \{ 2, 4, 6, 8, 10 \} \quad B = \{ x : x \text{ is positive even integer and } x \le 10 \} \)
\( A = \{ x : x \text{ is a multiple of } 10 \} \), \( B = \{ 10, 15, 20, 25, 30, \dots \} \)

▼

Answer:

Yes, \( A = B \). The order of elements does not matter in a set, and both contain exactly the same elements.
No, \( A \ne B \). \( 12 \in A \) but \( 12 \notin B \). Also \( 18 \in B \) but \( 18 \notin A \).
Yes, \( A = B \). The positive even integers less than or equal to 10 are 2, 4, 6, 8, 10. Thus, \( B = \{2, 4, 6, 8, 10\} \).
No, \( A \ne B \). Set A contains multiples of 10 only (10, 20, 30...), while Set B contains numbers like 15 and 25 which are not multiples of 10.

Are the following pair of sets equal? Give reasons.

\( A = \{2, 3\}, \quad B = \{x : x \text{ is solution of } x^2 + 5x + 6 = 0\} \)
\( A = \{ x : x \text{ is a letter in the word FOLLOW} \} \)
\( B = \{ y : y \text{ is a letter in the word WOLF} \} \)

▼

Answer:

No, \( A \ne B \).
Solving for set B: \( x^2 + 5x + 6 = 0 \)
\( (x + 2)(x + 3) = 0 \)
\( x = -2 \) or \( x = -3 \)
So, \( B = \{-2, -3\} \). Since \( \{2, 3\} \ne \{-2, -3\} \), the sets are not equal.
Yes, \( A = B \).
Listing elements of set A: \( \{F, O, L, W\} \) (repetitions are ignored).
Listing elements of set B: \( \{W, O, L, F\} \).
Both sets contain exactly the same letters.

From the sets given below, select equal sets:

\( A = \{ 2, 4, 8, 12\} \)

\( B = \{ 1, 2, 3, 4\} \)

\( C = \{ 4, 8, 12, 14\} \)

\( D = \{ 3, 1, 4, 2\} \)

\( E = \{ -1, 1\} \)

\( F = \{ 0, a\} \)

\( G = \{ 1, -1\} \)

\( H = \{ 0, 1\} \)

▼

Answer:

By comparing the elements of the given sets, we find:

Set \( B = \{1, 2, 3, 4\} \) and Set \( D = \{3, 1, 4, 2\} \). They have the exact same elements. So, \( B = D \).
Set \( E = \{-1, 1\} \) and Set \( G = \{1, -1\} \). They have the exact same elements. So, \( E = G \).

No other sets are equal.

Make correct statements by filling in the symbols \( \subset \) or \( \not\subset \) in the blank spaces:

\( \{ 2, 3, 4 \} \dots \{ 1, 2, 3, 4, 5 \} \)
\( \{ a, b, c \} \dots \{ b, c, d \} \)
\( \{ x : x \text{ is a student of Class XI of your school} \} \dots \{ x : x \text{ student of your school} \} \)
\( \{ x : x \text{ is a circle in the plane} \} \dots \{ x : x \text{ is a circle in the same plane with radius 1 unit} \} \)
\( \{ x : x \text{ is a triangle in a plane} \} \dots \{ x : x \text{ is a rectangle in the plane} \} \)
\( \{ x : x \text{ is an equilateral triangle in a plane} \} \dots \{ x : x \text{ is a triangle in the same plane} \} \)
\( \{ x : x \text{ is an even natural number} \} \dots \{ x : x \text{ is an integer} \} \)

▼

Answer:

\( \{ 2, 3, 4 \} \subset \{ 1, 2, 3, 4, 5 \} \)
(Every element of the first set is in the second set).
\( \{ a, b, c \} \not\subset \{ b, c, d \} \)
(Element 'a' belongs to the first set but not the second).
\( \subset \)
(Every student of Class XI is also a student of the school).
\( \not\subset \)
(The first set contains circles of all radii, while the second only contains circles of radius 1).
\( \not\subset \)
(A triangle is not a rectangle).
\( \subset \)
(Every equilateral triangle is a triangle).
\( \subset \)
(Every even natural number is an integer).

Examine whether the following statements are true or false:

\( \{ a, b \} \not\subset \{ b, c, a \} \)
\( \{ a, e \} \subset \{ x : x \text{ is a vowel in the English alphabet} \} \)
\( \{ 1, 2, 3 \} \subset \{ 1, 3, 5 \} \)
\( \{ a \} \subset \{ a, b, c \} \)
\( \{ a \} \in \{ a, b, c \} \)
\( \{ x : x \text{ is an even natural number less than 6} \} \subset \{ x : x \text{ is a natural number which divides 36} \} \)

▼

Answer:

False. Since every element of \(\{a, b\}\) is in \(\{b, c, a\}\), it should be \( \subset \).
True. 'a' and 'e' are both vowels.
False. The element 2 is in the LHS set but not in the RHS set.
True. 'a' is an element of the RHS set, so \(\{a\}\) is a subset.
False. \(\{a\}\) is a subset, not an element. The element is just 'a'.
True.
LHS = \(\{2, 4\}\)
RHS = Factors of 36 = \(\{1, 2, 3, 4, 6, 9, 12, 18, 36\}\)
Since 2 and 4 are in the RHS, the statement is true.

Let \( A = \{ 1, 2, \{ 3, 4 \}, 5 \} \). Which of the following statements are incorrect and why?

(i) \( \{ 3, 4 \} \subset A \)

(ii) \( \{ 3, 4 \} \in A \)

(iii) \( \{ \{ 3, 4 \} \} \subset A \)

(iv) \( 1 \in A \)

(v) \( 1 \subset A \)

(vi) \( \{ 1, 2, 5 \} \subset A \)

(vii) \( \{ 1, 2, 5 \} \in A \)

(viii) \( \{ 1, 2, 3 \} \subset A \)

(ix) \( \phi \in A \)

(x) \( \phi \subset A \)

(xi) \( \{ \phi \} \subset A \)

▼

Answer:

Note: The elements of \( A \) are \( 1, 2, \{3, 4\}, 5 \).

Incorrect. \( \{3, 4\} \) is an element of \( A \), not a subset. (Correct form: \( \{3, 4\} \in A \)).
Correct.
Correct. \( \{3, 4\} \) is an element, so putting it in braces makes it a subset containing that element.
Correct.
Incorrect. 1 is an element, not a set. An element cannot be a subset. (Correct form: \( \{1\} \subset A \)).
Correct. 1, 2, and 5 are elements of \( A \).
Incorrect. The group \(\{1, 2, 5\}\) is not listed as a single element inside \( A \).
Incorrect. 3 is not an element of \( A \). The element is \(\{3, 4\}\). Therefore, 3 cannot belong to a subset of \( A \).
Incorrect. \( \phi \) is not listed as an element in \( A \).
Correct. The null set is a subset of every set.
Incorrect. \( \phi \) is not an element of \( A \), so the set containing \( \phi \) is not a subset of \( A \).

Write down all the subsets of the following sets:

\( \{a\} \)
\( \{a, b\} \)
\( \{1, 2, 3\} \)
\( \phi \)

▼

Answer:

Subsets of \( \{a\} \):
\( \phi, \{a\} \)
Subsets of \( \{a, b\} \):
\( \phi, \{a\}, \{b\}, \{a, b\} \)
Subsets of \( \{1, 2, 3\} \):
\( \phi, \{1\}, \{2\}, \{3\}, \{1, 2\}, \{1, 3\}, \{2, 3\}, \{1, 2, 3\} \)
Subsets of \( \phi \):
\( \phi \)

Write the following as intervals:

\( \{ x : x \in \mathbb{R}, -4 < x \le 6 \} \)
\( \{ x : x \in \mathbb{R}, -12 < x < -10 \} \)
\( \{ x : x \in \mathbb{R}, 0 \le x < 7 \} \)
\( \{ x : x \in \mathbb{R}, 3 \le x \le 4 \} \)

▼

Answer:

\( (-4, 6] \)
\( (-12, -10) \)
\( [0, 7) \)
\( [3, 4] \)

Write the following intervals in set-builder form:

\( (-3, 0) \)
\( [6, 12] \)
\( (6, 12] \)
\( [-23, 5) \)

▼

Answer:

\( \{ x : x \in \mathbb{R}, -3 < x < 0 \} \)
\( \{ x : x \in \mathbb{R}, 6 \le x \le 12 \} \)
\( \{ x : x \in \mathbb{R}, 6 < x \le 12 \} \)
\( \{ x : x \in \mathbb{R}, -23 \le x < 5 \} \)

What universal set(s) would you propose for each of the following:

The set of right triangles.
The set of isosceles triangles.

▼

Answer:

For both cases, the universal set can be:

The set of all triangles.
The set of all polygons.
The set of all 2D geometrical figures.

Ideally: \( U = \{ x : x \text{ is a triangle} \} \).

Given the sets \( A = \{1, 3, 5\} \), \( B = \{2, 4, 6\} \) and \( C = \{0, 2, 4, 6, 8\} \), which of the following may be considered as universal set (s) for all the three sets A, B and C?

\( \{0, 1, 2, 3, 4, 5, 6\} \)
\( \phi \)
\( \{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10\} \)
\( \{1, 2, 3, 4, 5, 6, 7, 8\} \)

▼

Answer:

A universal set must contain all elements from sets A, B, and C combined.

Elements required: \( \{1, 3, 5\} \cup \{2, 4, 6\} \cup \{0, 2, 4, 6, 8\} = \{0, 1, 2, 3, 4, 5, 6, 8\} \).

Analysis of options:

Excluded (missing 8).
Excluded (empty).
Correct. This set contains all the required elements (0, 1, 2, 3, 4, 5, 6, 8) plus others.
Excluded (missing 0).

Find the union of each of the following pairs of sets:

\( X = \{1, 3, 5\} \quad Y = \{1, 2, 3\} \)
\( A = \{a, e, i, o, u\} \quad B = \{a, b, c\} \)
\( A = \{x : x \text{ is a natural number and multiple of 3}\} \)
\( B = \{x : x \text{ is a natural number less than 6}\} \)
\( A = \{x : x \text{ is a natural number and } 1 < x \le 6 \} \)
\( B = \{x : x \text{ is a natural number and } 6 < x < 10 \} \)
\( A = \{1, 2, 3\}, \quad B = \phi \)

▼

Answer:

\( X \cup Y = \{1, 2, 3, 5\} \)
\( A \cup B = \{a, b, c, e, i, o, u\} \)
\( A = \{3, 6, 9, \dots\} \), \( B = \{1, 2, 3, 4, 5\} \)
\( A \cup B = \{1, 2, 4, 5, 3, 6, 9, 12, \dots\} \) or
\( \{x : x = 1, 2, 4, 5 \text{ or } x \text{ is a multiple of 3}\} \)
\( A = \{2, 3, 4, 5, 6\} \), \( B = \{7, 8, 9\} \)
\( A \cup B = \{2, 3, 4, 5, 6, 7, 8, 9\} \)
\( A \cup B = \{1, 2, 3\} \)

Let \( A = \{a, b\}, B = \{a, b, c\} \). Is \( A \subset B \)? What is \( A \cup B \)?

▼

Answer:

Yes, \( A \subset B \). Every element of A ('a' and 'b') is present in set B.

\( A \cup B = \{a, b, c\} = B \)

If A and B are two sets such that \( A \subset B \), then what is \( A \cup B \)?

▼

Answer:

If \( A \subset B \), then all elements of A are already in B. Therefore, combining them adds no new elements to B.

\( A \cup B = B \)

If \( A = \{1, 2, 3, 4\}, B = \{3, 4, 5, 6\}, C = \{5, 6, 7, 8\} \) and \( D = \{7, 8, 9, 10\} \); find:

\( A \cup B \)
\( A \cup C \)
\( B \cup C \)
\( B \cup D \)
\( A \cup B \cup C \)
\( A \cup B \cup D \)
\( B \cup C \cup D \)

▼

Answer:

\( A \cup B = \{1, 2, 3, 4, 5, 6\} \)
\( A \cup C = \{1, 2, 3, 4, 5, 6, 7, 8\} \)
\( B \cup C = \{3, 4, 5, 6, 7, 8\} \)
\( B \cup D = \{3, 4, 5, 6, 7, 8, 9, 10\} \)
\( A \cup B \cup C = \{1, 2, 3, 4, 5, 6, 7, 8\} \)
\( A \cup B \cup D = \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10\} \)
\( B \cup C \cup D = \{3, 4, 5, 6, 7, 8, 9, 10\} \)

Find the intersection of each pair of sets of question 1 above.

▼

Answer:

\( X \cap Y = \{1, 3\} \)
\( A \cap B = \{a\} \)
\( A = \{3, 6, \dots\}, B = \{1, 2, 3, 4, 5\} \Rightarrow A \cap B = \{3\} \)
\( A = \{2, 3, 4, 5, 6\}, B = \{7, 8, 9\} \Rightarrow A \cap B = \phi \) (Disjoint)
\( A \cap B = \phi \) (Intersection with null set is null)

If \( A = \{3, 5, 7, 9, 11\}, B = \{7, 9, 11, 13\}, C = \{11, 13, 15\} \) and \( D = \{15, 17\} \); find:

\( A \cap B \)
\( B \cap C \)
\( A \cap C \cap D \)
\( A \cap C \)
\( B \cap D \)
\( A \cap (B \cup C) \)
\( A \cap D \)
\( A \cap (B \cup D) \)
\( (A \cap B) \cap (B \cup C) \)
\( (A \cup D) \cap (B \cup C) \)

▼

Answer:

\( \{7, 9, 11\} \)
\( \{11, 13\} \)
\( (A \cap C) = \{11\} \). Then \( \{11\} \cap D = \phi \). Answer: \( \phi \)
\( \{11\} \)
\( \phi \) (No common elements)
\( B \cup C = \{7, 9, 11, 13, 15\} \). Intersection with A: \( \{7, 9, 11\} \)
\( \phi \)
\( B \cup D = \{7, 9, 11, 13, 15, 17\} \). Intersection with A: \( \{7, 9, 11\} \)
\( A \cap B = \{7, 9, 11\} \). \( B \cup C = \{7, 9, 11, 13, 15\} \). Intersection: \( \{7, 9, 11\} \)
\( A \cup D = \{3, 5, 7, 9, 11, 15, 17\} \)
\( B \cup C = \{7, 9, 11, 13, 15\} \)
Intersection: \( \{7, 9, 11, 15\} \)

If \( A = \{x : x \text{ is a natural number}\} \), \( B = \{x : x \text{ is an even natural number}\} \), \( C = \{x : x \text{ is an odd natural number}\} \) and \( D = \{x : x \text{ is a prime number}\} \), find:

\( A \cap B \)
\( A \cap C \)
\( A \cap D \)
\( B \cap C \)
\( B \cap D \)
\( C \cap D \)

▼

Answer:

\( B \) (Intersection of all natural numbers and even natural numbers is even natural numbers)
\( C \) (Intersection of all natural numbers and odd natural numbers is odd natural numbers)
\( D \) (Intersection of all natural numbers and prime numbers is prime numbers)
\( \phi \) (A number cannot be both even and odd)
\( \{2\} \) (2 is the only even prime number)
\( \{x : x \text{ is an odd prime number}\} \) (All primes except 2)

Which of the following pairs of sets are disjoint?

\( \{1, 2, 3, 4\} \) and \( \{x : x \text{ is a natural number and } 4 \le x \le 6 \} \)
\( \{a, e, i, o, u\} \) and \( \{c, d, e, f\} \)
\( \{x : x \text{ is an even integer}\} \) and \( \{x : x \text{ is an odd integer}\} \)

▼

Answer:

Not Disjoint. Second set is \( \{4, 5, 6\} \). Common element: 4.
Not Disjoint. Common element: e.
Disjoint. No integer can be both even and odd. Intersection is \( \phi \).

If \( A = \{3, 6, 9, 12, 15, 18, 21\}, B = \{4, 8, 12, 16, 20\}, C = \{2, 4, 6, 8, 10, 12, 14, 16\}, D = \{5, 10, 15, 20\} \); find:

A – B
A – C
A – D
B – A
C – A
D – A
B – C
B – D
C – B
D – B
C – D
D – C

▼

Answer:

Difference A - B means elements belonging to A but NOT to B.

\( \{3, 6, 9, 15, 18, 21\} \) (Removed 12)
\( \{3, 9, 15, 18, 21\} \) (Removed 6, 12)
\( \{3, 6, 9, 12, 18, 21\} \) (Removed 15)
\( \{4, 8, 16, 20\} \) (Removed 12)
\( \{2, 4, 8, 10, 14, 16\} \) (Removed 6, 12)
\( \{5, 10, 20\} \) (Removed 15)
\( \{20\} \) (Removed 4, 8, 12, 16)
\( \{4, 8, 12, 16\} \) (Removed 20)
\( \{2, 6, 10, 14\} \) (Removed 4, 8, 12, 16)
\( \{5, 10, 15\} \) (Removed 20)
\( \{2, 4, 6, 8, 12, 14, 16\} \) (Removed 10)
\( \{5, 15, 20\} \) (Removed 10)

Q10

If \( X = \{a, b, c, d\} \) and \( Y = \{f, b, d, g\} \), find:

\( X - Y \)
\( Y - X \)
\( X \cap Y \)

▼

Answer:

\( \{a, c\} \) (Elements in X but not Y)
\( \{f, g\} \) (Elements in Y but not X)
\( \{b, d\} \) (Elements common to both)

Q11

If R is the set of real numbers and Q is the set of rational numbers, then what is R – Q?

▼

Answer:

The set of Real numbers (R) consists of Rational numbers (Q) and Irrational numbers (T or \(\mathbb{I}\)).

Therefore, \( R - Q \) is the set of all irrational numbers.

Q12

State whether each of the following statement is true or false. Justify your answer.

\( \{2, 3, 4, 5\} \) and \( \{3, 6\} \) are disjoint sets.
\( \{a, e, i, o, u\} \) and \( \{a, b, c, d\} \) are disjoint sets.
\( \{2, 6, 10, 14\} \) and \( \{3, 7, 11, 15\} \) are disjoint sets.
\( \{2, 6, 10\} \) and \( \{3, 7, 11\} \) are disjoint sets.

▼

Answer:

False. They share the element 3.
False. They share the element 'a'.
True. They have no common elements.
True. They have no common elements.

Let \( U = \{ 1, 2, 3, 4, 5, 6, 7, 8, 9 \}, A = \{ 1, 2, 3, 4 \}, B = \{ 2, 4, 6, 8 \} \) and \( C = \{ 3, 4, 5, 6 \} \). Find:

\( A' \)
\( B' \)
\( (A \cup C)' \)
\( (A \cup B)' \)
\( (A')' \)
\( (B - C)' \)

▼

Answer:

\( A' = U - A = \{5, 6, 7, 8, 9\} \)
\( B' = U - B = \{1, 3, 5, 7, 9\} \)
\( A \cup C = \{1, 2, 3, 4, 5, 6\} \)
\( (A \cup C)' = U - \{1, 2, 3, 4, 5, 6\} = \{7, 8, 9\} \)
\( A \cup B = \{1, 2, 3, 4, 6, 8\} \)
\( (A \cup B)' = U - \{1, 2, 3, 4, 6, 8\} = \{5, 7, 9\} \)
\( (A')' = A = \{1, 2, 3, 4\} \)
\( B - C \) (elements in B but not C) \( = \{2, 8\} \)
\( (B - C)' = U - \{2, 8\} = \{1, 3, 4, 5, 6, 7, 9\} \)

If \( U = \{ a, b, c, d, e, f, g, h \} \), find the complements of the following sets:

\( A = \{ a, b, c \} \)
\( B = \{ d, e, f, g \} \)
\( C = \{ a, c, e, g \} \)
\( D = \{ f, g, h, a \} \)

▼

Answer:

\( A' = \{d, e, f, g, h\} \)
\( B' = \{a, b, c, h\} \)
\( C' = \{b, d, f, h\} \)
\( D' = \{b, c, d, e\} \)

Taking the set of natural numbers as the universal set, write down the complements of the following sets:

\( \{x : x \text{ is an even natural number}\} \)
\( \{x : x \text{ is an odd natural number}\} \)
\( \{x : x \text{ is a positive multiple of 3}\} \)
\( \{x : x \text{ is a prime number}\} \)
\( \{x : x \text{ is a natural number divisible by 3 and 5}\} \)
\( \{x : x \text{ is a perfect square}\} \)
\( \{x : x \text{ is a perfect cube}\} \)
\( \{x : x + 5 = 8\} \)
\( \{x : 2x + 5 = 9\} \)
\( \{x : x \ge 7\} \)
\( \{x : x \in \mathbb{N} \text{ and } 2x + 1 > 10\} \)

▼

Answer:

Assuming \( U = \mathbb{N} \):

\( \{x : x \text{ is an odd natural number}\} \)
\( \{x : x \text{ is an even natural number}\} \)
\( \{x : x \in \mathbb{N} \text{ and } x \text{ is not a multiple of 3}\} \)
\( \{x : x \text{ is a positive composite number or } x = 1\} \)
Divisible by 3 and 5 means divisible by 15. Complement:
\( \{x : x \in \mathbb{N} \text{ and } x \text{ is not divisible by 15}\} \)
\( \{x : x \in \mathbb{N} \text{ and } x \text{ is not a perfect square}\} \)
\( \{x : x \in \mathbb{N} \text{ and } x \text{ is not a perfect cube}\} \)
Given set is \( \{3\} \). Complement is \( \{x : x \in \mathbb{N} \text{ and } x \ne 3\} \)
Solve \( 2x+5=9 \Rightarrow 2x=4 \Rightarrow x=2 \). Given set is \( \{2\} \).
Complement is \( \{x : x \in \mathbb{N} \text{ and } x \ne 2\} \)
Complement is \( \{x : x \in \mathbb{N} \text{ and } x < 7\} = \{1, 2, 3, 4, 5, 6\} \)
Solve \( 2x+1 > 10 \Rightarrow 2x > 9 \Rightarrow x > 4.5 \). The set is \( \{5, 6, 7, \dots\} \).
Complement is \( \{1, 2, 3, 4\} \)

If \( U = \{1, 2, 3, 4, 5, 6, 7, 8, 9\}, A = \{2, 4, 6, 8\} \) and \( B = \{2, 3, 5, 7\} \). Verify that:

\( (A \cup B)' = A' \cap B' \)
\( (A \cap B)' = A' \cup B' \)

▼

Answer:

First, find the complements:

\( A' = \{1, 3, 5, 7, 9\} \)
\( B' = \{1, 4, 6, 8, 9\} \)

(i) Verify \( (A \cup B)' = A' \cap B' \)

\( A \cup B = \{2, 3, 4, 5, 6, 7, 8\} \)
LHS: \( (A \cup B)' = \{1, 9\} \)
RHS: \( A' \cap B' = \{1, 3, 5, 7, 9\} \cap \{1, 4, 6, 8, 9\} = \{1, 9\} \)
Since LHS = RHS, verified.

(ii) Verify \( (A \cap B)' = A' \cup B' \)

\( A \cap B = \{2\} \)
LHS: \( (A \cap B)' = \{1, 3, 4, 5, 6, 7, 8, 9\} \)
RHS: \( A' \cup B' = \{1, 3, 4, 5, 6, 7, 8, 9\} \)
Since LHS = RHS, verified.

Draw appropriate Venn diagram for each of the following:

\( (A \cup B)' \)
\( A' \cap B' \)
\( (A \cap B)' \)
\( A' \cup B' \)

▼

Answer:

According to De Morgan's Laws, we know that:

\( (A \cup B)' = A' \cap B' \) (The complement of the union is the intersection of complements).
\( (A \cap B)' = A' \cup B' \) (The complement of the intersection is the union of complements).

Therefore, the Venn diagram for (i) is identical to (ii), and the diagram for (iii) is identical to (iv).

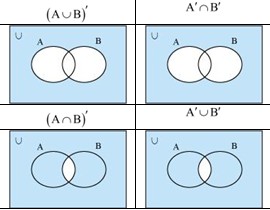
Description of Diagrams:

(i) & (ii): Draw a Universal box \( U \) with two overlapping circles \( A \) and \( B \). Shade the region outside both circles. This represents elements that are neither in A nor in B.
(iii) & (iv): Draw a Universal box \( U \) with two overlapping circles \( A \) and \( B \). Shade the entire box except for the small overlapping region in the center. This represents all elements except those common to both A and B.

Let U be the set of all triangles in a plane. If A is the set of all triangles with at least one angle different from \( 60^\circ \), what is \( A' \)?

▼

Answer:

Set A contains triangles where at least one angle is not \( 60^\circ \).

Therefore, the complement \( A' \) contains triangles where no angle is different from \( 60^\circ \). This means all three angles must be equal to \( 60^\circ \).

\( A' = \) The set of all equilateral triangles.

Fill in the blanks to make each of the following a true statement:

\( A \cup A' = \dots \)
\( \phi' \cap A = \dots \)
\( A \cap A' = \dots \)
\( U' \cap A = \dots \)

▼

Answer:

\( A \cup A' = \textbf{U} \) (Union of a set and its complement is the Universal set)
\( \phi' \cap A = U \cap A = \textbf{A} \) (Intersection of Universal set and A is A)
\( A \cap A' = \boldsymbol{\phi} \) (A set and its complement share no common elements)
\( U' \cap A = \phi \cap A = \boldsymbol{\phi} \) (Intersection with null set is null)

Decide, among the following sets, which sets are subsets of one and another:
\( A = \{ x : x \in \mathbf{R} \text{ and } x \text{ satisfy } x^2 - 8x + 12 = 0 \} \),
\( B = \{ 2, 4, 6 \} \),
\( C = \{ 2, 4, 6, 8, \dots \} \),
\( D = \{ 6 \} \).

▼

Answer:

First, let's write set A in roster form by solving the equation:

\( x^2 - 8x + 12 = 0 \)

\( (x - 2)(x - 6) = 0 \)

\( x = 2, 6 \)

So, \( A = \{ 2, 6 \} \).

Now we have:

\( A = \{ 2, 6 \} \)
\( B = \{ 2, 4, 6 \} \)
\( C = \{ 2, 4, 6, 8, \dots \} \) (Set of all even natural numbers)
\( D = \{ 6 \} \)

Subset Relationships:

\( D \subset A \) (Since \( \{6\} \subset \{2, 6\} \))
\( D \subset B \) (Since \( \{6\} \subset \{2, 4, 6\} \))
\( D \subset C \) (Since 6 is an even natural number)
\( A \subset B \) (Since \( \{2, 6\} \subset \{2, 4, 6\} \))
\( A \subset C \) (Since both 2 and 6 are even natural numbers)
\( B \subset C \) (Since all elements of B are even natural numbers)

In each of the following, determine whether the statement is true or false. If it is true, prove it. If it is false, give an example.

If \( x \in A \) and \( A \in B \), then \( x \in B \)
If \( A \subset B \) and \( B \in C \), then \( A \in C \)
If \( A \subset B \) and \( B \subset C \), then \( A \subset C \)
If \( A \not\subset B \) and \( B \not\subset C \), then \( A \not\subset C \)
If \( x \in A \) and \( A \not\subset B \), then \( x \in B \)
If \( A \subset B \) and \( x \notin B \), then \( x \notin A \)

▼

Answer:

False.
Let \( A = \{1\} \) and \( B = \{ \{1\}, 2 \} \).
Here \( 1 \in A \) and \( A \in B \), but \( 1 \notin B \) (the element of B is the set \( \{1\} \), not the number 1).
False.
Let \( A = \{1\} \), \( B = \{1, 2\} \), and \( C = \{ \{1, 2\}, 3 \} \).
Here \( A \subset B \) and \( B \in C \), but \( A \notin C \) (only the set \( \{1, 2\} \) is in C).
True.
Let \( x \) be an arbitrary element of \( A \).
Since \( A \subset B \), \( x \in B \).
Since \( B \subset C \), \( x \in C \).
Therefore, \( A \subset C \).
False.
Let \( A = \{1\} \), \( B = \{2\} \), and \( C = \{1, 5\} \).
\( A \not\subset B \) and \( B \not\subset C \).
However, \( A \subset C \) is true. Thus, the statement is false.
False.
Let \( A = \{1, 2\} \) and \( B = \{2, 3\} \).
\( 1 \in A \) and \( A \not\subset B \).
However, \( 1 \notin B \).
True.
We are given \( A \subset B \). Suppose \( x \in A \).
Then \( x \) must be in \( B \) (by definition of subset).
But we are given \( x \notin B \), so \( x \) cannot be in \( A \).
Therefore, \( x \notin A \).

Let A, B, and C be the sets such that \( A \cup B = A \cup C \) and \( A \cap B = A \cap C \). Show that \( B = C \).

▼

Answer:

Let \( x \in B \).

\( \Rightarrow x \in A \cup B \)

\( \Rightarrow x \in A \cup C \) (Given \( A \cup B = A \cup C \))

\( \Rightarrow x \in A \) or \( x \in C \)

Case 1: If \( x \in A \)
Since \( x \) was also in \( B \), then \( x \in A \cap B \).
Given \( A \cap B = A \cap C \), so \( x \in A \cap C \).
This implies \( x \in C \).

Case 2: If \( x \in C \)
Then directly \( x \in C \).

In both cases, \( B \subseteq C \).

Similarly, we can show \( C \subseteq B \).

Therefore, \( B = C \).

Show that the following four conditions are equivalent:

\( A \subset B \)
\( A - B = \phi \)
\( A \cup B = B \)
\( A \cap B = A \)

▼

Answer:

To show equivalence, we show logical implication in a cycle:

(i) \( \Rightarrow \) (ii):
If \( A \subset B \), every element of A is in B. Therefore, there are no elements in A that are not in B. Thus, \( A - B = \phi \).

(ii) \( \Rightarrow \) (iii):
If \( A - B = \phi \), then A contains no elements outside of B. This implies \( A \subset B \).
Therefore, the union \( A \cup B \) adds nothing new to B, so \( A \cup B = B \).

(iii) \( \Rightarrow \) (iv):
If \( A \cup B = B \), then all elements of A are contained within B.
The intersection of A and B will therefore be just the elements of A itself. So \( A \cap B = A \).

(iv) \( \Rightarrow \) (i):
If \( A \cap B = A \), it means all elements of A are also elements of B. Hence, \( A \subset B \).

Show that if \( A \subset B \), then \( C - B \subset C - A \).

▼

Answer:

Let \( x \) be an arbitrary element of \( C - B \).

\( \Rightarrow x \in C \) and \( x \notin B \).

Since \( A \subset B \), if an element is not in B, it cannot be in A (if it were in A, it would have to be in B).

\( \Rightarrow x \notin A \).

So, we have \( x \in C \) and \( x \notin A \).

\( \Rightarrow x \in C - A \).

Thus, \( C - B \subset C - A \).

Show that for any sets A and B, \( A = (A \cap B) \cup (A - B) \) and \( A \cup (B - A) = (A \cup B) \).

▼

Answer:

Part 1: Show \( A = (A \cap B) \cup (A - B) \)

RHS = \( (A \cap B) \cup (A \cap B') \)

= \( A \cap (B \cup B') \) (Distributive Law)

= \( A \cap U \) (Where U is universal set)

= \( A \)

So, LHS = RHS.

Part 2: Show \( A \cup (B - A) = (A \cup B) \)

LHS = \( A \cup (B \cap A') \)

= \( (A \cup B) \cap (A \cup A') \) (Distributive Law)

= \( (A \cup B) \cap U \)

= \( A \cup B \)

So, LHS = RHS.

Using properties of sets, show that:

\( A \cup (A \cap B) = A \)
\( A \cap (A \cup B) = A \)

▼

Answer:

(i) \( A \cup (A \cap B) = A \)

Since \( A \cap B \subset A \), the union of A with its own subset is just A.

Alternatively: \( A \cup (A \cap B) = (A \cap U) \cup (A \cap B) = A \cap (U \cup B) = A \cap U = A \).

(ii) \( A \cap (A \cup B) = A \)

Since \( A \subset (A \cup B) \), the intersection of A with its superset is just A.

Alternatively: \( A \cap (A \cup B) = (A \cup \phi) \cap (A \cup B) = A \cup (\phi \cap B) = A \cup \phi = A \).

Show that \( A \cap B = A \cap C \) need not imply \( B = C \).

▼

Answer:

We can prove this by counter-example.

Let \( A = \{1, 2\} \)

Let \( B = \{1, 3\} \)

Let \( C = \{1, 4\} \)

Then:

\( A \cap B = \{1\} \)
\( A \cap C = \{1\} \)

So \( A \cap B = A \cap C \), but clearly \( B \neq C \) (since \( 3 \in B \) but \( 3 \notin C \)).

Let A and B be sets. If \( A \cap X = B \cap X = \phi \) and \( A \cup X = B \cup X \) for some set X, show that \( A = B \).

▼

Answer:

Given \( A \cup X = B \cup X \).

Take intersection with A on both sides:

\( A \cap (A \cup X) = A \cap (B \cup X) \)

\( A = (A \cap B) \cup (A \cap X) \) (Using Absorption law on LHS and Distributive on RHS)

Since \( A \cap X = \phi \):

\( A = (A \cap B) \cup \phi \)

\( A = A \cap B \quad \dots(1) \)

Now, take intersection with B on both sides of \( A \cup X = B \cup X \):

\( B \cap (A \cup X) = B \cap (B \cup X) \)

\( (B \cap A) \cup (B \cap X) = B \)

Since \( B \cap X = \phi \):

\( (B \cap A) \cup \phi = B \)

\( A \cap B = B \quad \dots(2) \)

From (1) and (2), \( A = A \cap B \) and \( B = A \cap B \).

Therefore, \( A = B \).

Q10

Find sets A, B and C such that \( A \cap B, B \cap C \) and \( A \cap C \) are non-empty sets and \( A \cap B \cap C = \phi \).

▼

Answer:

We need pairs to share elements, but no element shared by all three.

Let:

\( A = \{1, 2\} \)
\( B = \{2, 3\} \)
\( C = \{1, 3\} \)

Check Intersections:

\( A \cap B = \{2\} \ne \phi \)
\( B \cap C = \{3\} \ne \phi \)
\( A \cap C = \{1\} \ne \phi \)

Check Common Intersection:

\( A \cap B \cap C = \{2\} \cap \{1, 3\} = \phi \)

The condition is satisfied.