Class 12- Applied Mathematics-NCERT Handbook Solutions-Unit-3(a)-Differentiation and its Applications -

NCERT Handbook Solutions

Class 12-Applied Mathematics (Unit-3-a)

EXERCISE 3.1

Find \( \frac{dy}{dx} \) from the following:
i. \( x^3 + y^3 = 3axy \)
ii. \( e^{xy} - 4xy = 4 \)
iii. \( 3x^3 - 5x^2y + 2xy^2 + 4y^3 = 0 \)
iv. \( x^{1/3} + y^{1/3} = a^{2/3} \) v. \( x = y\log(xy) \)

▼

i. \( x^3 + y^3 = 3axy \)

Differentiating both sides with respect to \( x \):

\[ \frac{d}{dx}(x^3) + \frac{d}{dx}(y^3) = \frac{d}{dx}(3axy) \] \[ 3x^2 + 3y^2 \frac{dy}{dx} = 3a \left[ y \cdot 1 + x \frac{dy}{dx} \right] \]

Divide by 3:

\[ x^2 + y^2 \frac{dy}{dx} = ay + ax \frac{dy}{dx} \] \[ y^2 \frac{dy}{dx} - ax \frac{dy}{dx} = ay - x^2 \] \[ \frac{dy}{dx} (y^2 - ax) = ay - x^2 \] \[ \frac{dy}{dx} = \frac{ay - x^2}{y^2 - ax} \]

ii. \( e^{xy} - 4xy = 4 \)

Differentiating both sides with respect to \( x \):

\[ \frac{d}{dx}(e^{xy}) - 4\frac{d}{dx}(xy) = \frac{d}{dx}(4) \] \[ e^{xy} \left( y + x\frac{dy}{dx} \right) - 4 \left( y + x\frac{dy}{dx} \right) = 0 \] \[ \left( e^{xy} - 4 \right) \left( y + x\frac{dy}{dx} \right) = 0 \]

Since \( e^{xy} - 4 = 4xy \) (from the original equation), generally \( e^{xy} - 4 \neq 0 \), so:

\[ y + x\frac{dy}{dx} = 0 \Rightarrow x\frac{dy}{dx} = -y \Rightarrow \frac{dy}{dx} = -\frac{y}{x} \]

iii. \( 3x^3 - 5x^2y + 2xy^2 + 4y^3 = 0 \)

Differentiating with respect to \( x \):

\[ 9x^2 - 5\left(2xy + x^2\frac{dy}{dx}\right) + 2\left(y^2 + 2xy\frac{dy}{dx}\right) + 12y^2\frac{dy}{dx} = 0 \] \[ 9x^2 - 10xy - 5x^2\frac{dy}{dx} + 2y^2 + 4xy\frac{dy}{dx} + 12y^2\frac{dy}{dx} = 0 \]

Grouping terms with \( \frac{dy}{dx} \):

\[ \frac{dy}{dx}(12y^2 + 4xy - 5x^2) = 10xy - 9x^2 - 2y^2 \] \[ \frac{dy}{dx} = \frac{10xy - 9x^2 - 2y^2}{12y^2 + 4xy - 5x^2} \]

iv. \( x^{1/3} + y^{1/3} = a^{2/3} \)

Differentiating with respect to \( x \):

\[ \frac{1}{3}x^{-2/3} + \frac{1}{3}y^{-2/3}\frac{dy}{dx} = 0 \] \[ x^{-2/3} + y^{-2/3}\frac{dy}{dx} = 0 \] \[ \frac{1}{x^{2/3}} + \frac{1}{y^{2/3}}\frac{dy}{dx} = 0 \] \[ \frac{dy}{dx} = -\frac{y^{2/3}}{x^{2/3}} = -\left(\frac{y}{x}\right)^{2/3} \]

v. \( x = y\log(xy) \)

Simplify using log properties: \( x = y(\log x + \log y) \)

Differentiating with respect to \( x \):

\[ 1 = \frac{dy}{dx}(\log x + \log y) + y\left( \frac{1}{x} + \frac{1}{y}\frac{dy}{dx} \right) \] \[ 1 = \frac{dy}{dx}\log(xy) + \frac{y}{x} + \frac{dy}{dx} \] \[ 1 - \frac{y}{x} = \frac{dy}{dx}(1 + \log(xy)) \]

From the original equation, \( \log(xy) = \frac{x}{y} \). Substitute this back:

\[ \frac{x-y}{x} = \frac{dy}{dx}\left(1 + \frac{x}{y}\right) \] \[ \frac{x-y}{x} = \frac{dy}{dx}\left(\frac{y+x}{y}\right) \] \[ \frac{dy}{dx} = \frac{y(x-y)}{x(x+y)} \]

Find \( \frac{dy}{dx} \) from the following parametric equations:
i. \( x = at, \quad y = \frac{a}{t} \)
ii. \( x = t \cdot \log t, \quad y = \frac{\log t}{t} \)
iii. \( x = \frac{a(1-t^2)}{1+t^2}, \quad y = \frac{2bt}{1+t^2} \)

▼

i. \( x = at, \quad y = \frac{a}{t} \)

\[ \frac{dx}{dt} = a, \quad \frac{dy}{dt} = -\frac{a}{t^2} \] \[ \frac{dy}{dx} = \frac{dy/dt}{dx/dt} = \frac{-a/t^2}{a} = -\frac{1}{t^2} \]

ii. \( x = t \cdot \log t, \quad y = \frac{\log t}{t} \)

\[ \frac{dx}{dt} = 1 \cdot \log t + t \cdot \frac{1}{t} = 1 + \log t \] \[ \frac{dy}{dt} = \frac{t(\frac{1}{t}) - \log t(1)}{t^2} = \frac{1 - \log t}{t^2} \] \[ \frac{dy}{dx} = \frac{dy/dt}{dx/dt} = \frac{1 - \log t}{t^2(1 + \log t)} \]

iii. \( x = \frac{a(1-t^2)}{1+t^2}, \quad y = \frac{2bt}{1+t^2} \)

Using quotient rule for differentiation:

\[ \frac{dx}{dt} = a \left[ \frac{(1+t^2)(-2t) - (1-t^2)(2t)}{(1+t^2)^2} \right] = a \left[ \frac{-2t - 2t^3 - 2t + 2t^3}{(1+t^2)^2} \right] = \frac{-4at}{(1+t^2)^2} \] \[ \frac{dy}{dt} = 2b \left[ \frac{(1+t^2)(1) - t(2t)}{(1+t^2)^2} \right] = 2b \left[ \frac{1+t^2-2t^2}{(1+t^2)^2} \right] = \frac{2b(1-t^2)}{(1+t^2)^2} \] \[ \frac{dy}{dx} = \frac{dy/dt}{dx/dt} = \frac{2b(1-t^2)}{(1+t^2)^2} \times \frac{(1+t^2)^2}{-4at} = -\frac{b(1-t^2)}{2at} \]

Find \( \frac{dy}{dx} \) from the following equations:
i. \( x^y = y^x \)
ii. \( x^y = e^{x-y} \)
iii. \( (x-y)e^{\frac{x}{x-y}} = 7 \)
iv. \( y = x^{\log x} \)

▼

i. \( x^y = y^x \)

Taking log on both sides: \( y \log x = x \log y \)

Differentiating w.r.t \( x \):

\[ \frac{dy}{dx}\log x + y\frac{1}{x} = 1 \cdot \log y + x \frac{1}{y}\frac{dy}{dx} \] \[ \frac{dy}{dx}\left(\log x - \frac{x}{y}\right) = \log y - \frac{y}{x} \] \[ \frac{dy}{dx}\left(\frac{y\log x - x}{y}\right) = \frac{x\log y - y}{x} \] \[ \frac{dy}{dx} = \frac{y(x\log y - y)}{x(y\log x - x)} \]

ii. \( x^y = e^{x-y} \)

Taking log on both sides: \( y \log x = (x-y)\log e = x-y \)

\[ y(1 + \log x) = x \Rightarrow y = \frac{x}{1 + \log x} \]

Differentiating using quotient rule:

\[ \frac{dy}{dx} = \frac{(1+\log x)(1) - x(\frac{1}{x})}{(1+\log x)^2} = \frac{1 + \log x - 1}{(1+\log x)^2} = \frac{\log x}{(1+\log x)^2} \]

iii. \( (x-y)e^{\frac{x}{x-y}} = 7 \)

Taking log on both sides:

\[ \log(x-y) + \frac{x}{x-y} = \log 7 \]

Let \( u = x-y \). Then \( \log u + \frac{x}{u} = \log 7 \).

Differentiating w.r.t \( x \):

\[ \frac{1}{u}\frac{du}{dx} + \frac{u(1) - x\frac{du}{dx}}{u^2} = 0 \]

Multiplying by \( u^2 \):

\[ u\frac{du}{dx} + u - x\frac{du}{dx} = 0 \Rightarrow \frac{du}{dx}(u-x) = -u \] \[ \frac{du}{dx} = \frac{-u}{u-x} = \frac{u}{x-u} \]

Since \( u = x-y \), \( \frac{du}{dx} = 1 - \frac{dy}{dx} \). Also \( x-u = x-(x-y) = y \).

\[ 1 - \frac{dy}{dx} = \frac{x-y}{y} \Rightarrow \frac{dy}{dx} = 1 - \frac{x-y}{y} = \frac{y - x + y}{y} = \frac{2y-x}{y} \]

iv. \( y = x^{\log x} \)

Taking log: \( \log y = \log x \cdot \log x = (\log x)^2 \)

Differentiating:

\[ \frac{1}{y}\frac{dy}{dx} = 2\log x \cdot \frac{1}{x} \] \[ \frac{dy}{dx} = y \cdot \frac{2\log x}{x} = x^{\log x} \frac{2\log x}{x} \]

Find \( \frac{d^2y}{dx^2} \) from the following:
(i) \( y = x\log x \)
(ii) \( y = x^2 e^x \)
(iii) \( y = \log(\log x) \)
(iv) \( y = 3e^{2x} + 2e^{3x} \)

▼

(i) \( y = x\log x \)

\[ \frac{dy}{dx} = 1 \cdot \log x + x \cdot \frac{1}{x} = \log x + 1 \] \[ \frac{d^2y}{dx^2} = \frac{1}{x} \]

(ii) \( y = x^2 e^x \)

\[ \frac{dy}{dx} = 2x e^x + x^2 e^x = e^x(x^2 + 2x) \] \[ \frac{d^2y}{dx^2} = e^x(x^2 + 2x) + e^x(2x + 2) = e^x(x^2 + 4x + 2) \]

(iii) \( y = \log(\log x) \)

\[ \frac{dy}{dx} = \frac{1}{\log x} \cdot \frac{1}{x} = (x \log x)^{-1} \] \[ \frac{d^2y}{dx^2} = -1(x \log x)^{-2} \cdot \frac{d}{dx}(x \log x) = -(x \log x)^{-2} (1 + \log x) = -\frac{1 + \log x}{(x \log x)^2} \]

(iv) \( y = 3e^{2x} + 2e^{3x} \)

\[ \frac{dy}{dx} = 3(2e^{2x}) + 2(3e^{3x}) = 6e^{2x} + 6e^{3x} \] \[ \frac{d^2y}{dx^2} = 6(2e^{2x}) + 6(3e^{3x}) = 12e^{2x} + 18e^{3x} \]

If \( x\sqrt{1+y} + y\sqrt{1+x} = 0 \), show that \( (1+x^2)\frac{dy}{dx} + 1 = 0 \).

▼

Proof:

Given \( x\sqrt{1+y} = -y\sqrt{1+x} \). Squaring both sides:

\[ x^2(1+y) = y^2(1+x) \] \[ x^2 + x^2y = y^2 + y^2x \] \[ x^2 - y^2 = xy(y - x) \] \[ (x-y)(x+y) = -xy(x-y) \]

Dividing by \( (x-y) \) (since \( x \neq y \)):

\[ x+y = -xy \Rightarrow y(1+x) = -x \Rightarrow y = -\frac{x}{1+x} \]

Differentiating w.r.t \( x \):

\[ \frac{dy}{dx} = -\left[ \frac{(1+x)(1) - x(1)}{(1+x)^2} \right] = -\frac{1}{(1+x)^2} \]

Note: The standard form of this question is to show \( (1+x)^2\frac{dy}{dx} + 1 = 0 \). Based on our derivation:

\[ (1+x)^2\frac{dy}{dx} = (1+x)^2 \left( -\frac{1}{(1+x)^2} \right) = -1 \] \[ (1+x)^2\frac{dy}{dx} + 1 = 0 \]

The question text in the image has a typo: \( (1+x^2) \) instead of \( (1+x)^2 \).

If \( y^{1/m} + y^{-1/m} = 2x \) then prove that \( (x^2-1)y_1^2 = m^2y^2 \).

▼

Proof:

Differentiating the given equation w.r.t \( x \) (where \( y_1 = \frac{dy}{dx} \)):

\[ \frac{1}{m}y^{\frac{1}{m}-1}y_1 - \frac{1}{m}y^{-\frac{1}{m}-1}y_1 = 2 \] \[ \frac{y_1}{m} \left( \frac{y^{1/m}}{y} - \frac{y^{-1/m}}{y} \right) = 2 \] \[ \frac{y_1}{my} (y^{1/m} - y^{-1/m}) = 2 \] \[ y_1 (y^{1/m} - y^{-1/m}) = 2my \]

Squaring both sides:

\[ y_1^2 (y^{1/m} - y^{-1/m})^2 = 4m^2y^2 \]

Using the identity \( (a-b)^2 = (a+b)^2 - 4ab \), with \( a=y^{1/m} \) and \( b=y^{-1/m} \):

\[ (y^{1/m} - y^{-1/m})^2 = (y^{1/m} + y^{-1/m})^2 - 4(y^{1/m} \cdot y^{-1/m}) \] \[ = (2x)^2 - 4(1) = 4x^2 - 4 = 4(x^2 - 1) \]

Substituting this back:

\[ y_1^2 [4(x^2 - 1)] = 4m^2y^2 \] \[ (x^2 - 1)y_1^2 = m^2y^2 \]

Hence Proved.

If \( y = \log(x + \sqrt{a^2+x^2}) \), show that \( (a^2+x^2)y_2 + xy_1 = 0 \).

▼

Proof:

Differentiating \( y \) w.r.t \( x \):

\[ y_1 = \frac{1}{x + \sqrt{a^2+x^2}} \left( 1 + \frac{2x}{2\sqrt{a^2+x^2}} \right) \] \[ y_1 = \frac{1}{x + \sqrt{a^2+x^2}} \left( \frac{\sqrt{a^2+x^2} + x}{\sqrt{a^2+x^2}} \right) = \frac{1}{\sqrt{a^2+x^2}} \]

Cross-multiplying:

\[ \sqrt{a^2+x^2} y_1 = 1 \]

Squaring both sides:

\[ (a^2+x^2)y_1^2 = 1 \]

Differentiating again w.r.t \( x \):

\[ (a^2+x^2) \cdot 2y_1 y_2 + y_1^2 \cdot (2x) = 0 \]

Dividing by \( 2y_1 \) (since \( y_1 \neq 0 \)):

\[ (a^2+x^2)y_2 + xy_1 = 0 \]

Hence Proved.

If \( y = (x + \sqrt{x^2+1})^p \), prove that \( (x^2+1)y_2 + xy_1 - p^2y = 0 \).

▼

Proof:

Differentiating \( y \) w.r.t \( x \):

\[ y_1 = p(x + \sqrt{x^2+1})^{p-1} \left( 1 + \frac{x}{\sqrt{x^2+1}} \right) \] \[ y_1 = p(x + \sqrt{x^2+1})^{p-1} \left( \frac{\sqrt{x^2+1}+x}{\sqrt{x^2+1}} \right) \] \[ y_1 = \frac{p(x + \sqrt{x^2+1})^{p}}{\sqrt{x^2+1}} = \frac{py}{\sqrt{x^2+1}} \]

Cross-multiplying:

\[ \sqrt{x^2+1} y_1 = py \]

Squaring both sides:

\[ (x^2+1)y_1^2 = p^2y^2 \]

Differentiating again w.r.t \( x \):

\[ (x^2+1) \cdot 2y_1 y_2 + y_1^2(2x) = p^2 \cdot 2y y_1 \]

Dividing entire equation by \( 2y_1 \):

\[ (x^2+1)y_2 + xy_1 = p^2y \] \[ (x^2+1)y_2 + xy_1 - p^2y = 0 \]

Hence Proved.

EXERCISE 3.2

Find the rate of change of circumference of a circle with respect to the radius \( r \).

▼

Answer: \( 2\pi \)

The circumference \( C \) of a circle is given by:

\[ C = 2\pi r \]

We need to find the rate of change of circumference with respect to radius \( r \), which is \( \frac{dC}{dr} \):

\[ \frac{dC}{dr} = \frac{d}{dr}(2\pi r) = 2\pi \]

Find the rate of change of lateral surface area of a cube with respect to side \( x \), when \( x = 4 \) cm.

▼

Answer: 32 cm

The lateral surface area \( A \) of a cube with side \( x \) is the area of 4 walls:

\[ A = 4x^2 \]

The rate of change with respect to \( x \) is \( \frac{dA}{dx} \):

\[ \frac{dA}{dx} = 8x \]

At \( x = 4 \) cm:

\[ \left. \frac{dA}{dx} \right|_{x=4} = 8(4) = 32 \text{ cm} \]

If the rate of change of volume of a sphere is equal to the rate of change of its radius, then find its radius. Also find its surface area.

▼

Answer: Radius = \( \frac{1}{2\sqrt{\pi}} \); Rate of change of Surface Area = \( 4\sqrt{\pi} \)

Let \( V \) be the volume and \( r \) be the radius.

\[ V = \frac{4}{3}\pi r^3 \]

Differentiating with respect to time \( t \):

\[ \frac{dV}{dt} = 4\pi r^2 \frac{dr}{dt} \]

Given that the rate of change of volume is equal to the rate of change of radius (\( \frac{dV}{dt} = \frac{dr}{dt} \)):

\[ \frac{dr}{dt} = 4\pi r^2 \frac{dr}{dt} \]

Assuming \( \frac{dr}{dt} \neq 0 \), we divide by it:

\[ 1 = 4\pi r^2 \implies r^2 = \frac{1}{4\pi} \implies r = \frac{1}{2\sqrt{\pi}} \]

Rate of change of Surface Area (\( S \)):

\[ S = 4\pi r^2 \]

We interpret the second part as finding the rate of change of surface area under the same condition (equivalent to finding \( \frac{dS}{dr} \) given the unit rate relationship implies derivatives w.r.t radius behave as unity relative to volume rate):

\[ \frac{dS}{dt} = 8\pi r \frac{dr}{dt} \]

Since \( \frac{dV}{dt} = \frac{dr}{dt} \), let's assume this common rate is \( k \). Then \( \frac{dS}{dt} = 8\pi r k \). If we consider the rate of change with respect to the radius (where \( \frac{dr}{dr} = 1 \)):

\[ \frac{dS}{dr} = 8\pi r = 8\pi \left( \frac{1}{2\sqrt{\pi}} \right) = 4\sqrt{\pi} \]

The volume of a cone changes at the rate 40 cm\(^3\)/sec. If height of the cone is always equal to its diameter, then find the rate of change of radius when its circular base area is 1 m\(^2\).

▼

Answer: 0.002 cm/sec

1. Setup the Volume equation:
Let radius be \( r \) and height be \( h \).
Given: \( h = \text{diameter} = 2r \).
Volume \( V = \frac{1}{3}\pi r^2 h = \frac{1}{3}\pi r^2 (2r) = \frac{2}{3}\pi r^3 \).

2. Differentiate with respect to time \( t \):

\[ \frac{dV}{dt} = \frac{2}{3}\pi (3r^2) \frac{dr}{dt} = 2\pi r^2 \frac{dr}{dt} \]

3. Substitute given values:
Given \( \frac{dV}{dt} = 40 \) cm\(^3\)/sec.
Base Area \( \pi r^2 = 1 \text{ m}^2 = 10,000 \text{ cm}^2 \). (Note: \( 1 \text{ m} = 100 \text{ cm} \), so \( 1 \text{ m}^2 = 100^2 \text{ cm}^2 \)).
Substitute \( \pi r^2 = 10000 \) into the derivative equation:

\[ 40 = 2(\pi r^2) \frac{dr}{dt} \] \[ 40 = 2(10000) \frac{dr}{dt} \] \[ 40 = 20000 \frac{dr}{dt} \] \[ \frac{dr}{dt} = \frac{40}{20000} = \frac{1}{500} = 0.002 \text{ cm/sec} \]

For what values of \( x \) is the rate of increase of total cost function \( C(x) = x^3 - 5x^2 + 5x + 8 \) is twice the rate of increase of \( x \)?
(Note: The question text in the image contains a typo "x^3 - 5x + 5x + 8". The standard form "x^3 - 5x^2 + 5x + 8" is used here for a valid solution.)

▼

Answer: \( x = \frac{1}{3}, 3 \)

Let rate of increase of \( x \) be \( \frac{dx}{dt} \). Then the rate of increase of cost is \( \frac{dC}{dt} \).

Given condition: \( \frac{dC}{dt} = 2 \frac{dx}{dt} \).

Using Chain Rule: \( \frac{dC}{dt} = C'(x) \frac{dx}{dt} \).

Therefore: \( C'(x) \frac{dx}{dt} = 2 \frac{dx}{dt} \implies C'(x) = 2 \).

Differentiating \( C(x) = x^3 - 5x^2 + 5x + 8 \):

\[ 3x^2 - 10x + 5 = 2 \] \[ 3x^2 - 10x + 3 = 0 \]

Factorizing the quadratic equation:

\[ 3x^2 - 9x - x + 3 = 0 \] \[ 3x(x - 3) - 1(x - 3) = 0 \] \[ (3x - 1)(x - 3) = 0 \]

So, \( x = \frac{1}{3} \) or \( x = 3 \).

The radius of the base of a cone is increasing at the rate of 3cm/minute and the altitude is decreasing at the rate of 4cm/minute. Find the rate of change of lateral surface area when the radius is 7cm and the altitude 24 cm.

▼

Answer: \( 54\pi \text{ cm}^2/\text{min} \)

Let radius be \( r \) and altitude be \( h \). Lateral Surface Area \( S = \pi r l = \pi r \sqrt{r^2 + h^2} \).

Given:
\( \frac{dr}{dt} = 3 \)
\( \frac{dh}{dt} = -4 \) (decreasing)
At instant: \( r = 7 \), \( h = 24 \).

First, find slant height \( l \):

\[ l = \sqrt{7^2 + 24^2} = \sqrt{49 + 576} = \sqrt{625} = 25 \]

Differentiating \( S \) with respect to \( t \):

\[ \frac{dS}{dt} = \pi \left[ \frac{dr}{dt} \sqrt{r^2+h^2} + r \cdot \frac{d}{dt}(\sqrt{r^2+h^2}) \right] \] \[ \frac{dS}{dt} = \pi \left[ \frac{dr}{dt} l + r \cdot \frac{1}{2\sqrt{r^2+h^2}}(2r\frac{dr}{dt} + 2h\frac{dh}{dt}) \right] \] \[ \frac{dS}{dt} = \pi \left[ 3(25) + \frac{7}{25}(7(3) + 24(-4)) \right] \] \[ = \pi \left[ 75 + \frac{7}{25}(21 - 96) \right] \] \[ = \pi \left[ 75 + \frac{7}{25}(-75) \right] \] \[ = \pi [ 75 - 21 ] = 54\pi \]

A ladder 10 meters long rests with one end against a vertical wall, the other on the floor. The lower end moves away from the wall at the rate of 2 meters / minute. Find the rate at which the upper end falls when its base is 6 meters away from the wall.

▼

Answer: 1.5 m/min

Let \( x \) be the distance from the wall (base) and \( y \) be the height on the wall. Length is 10 m.

\[ x^2 + y^2 = 10^2 = 100 \]

Differentiating w.r.t \( t \):

\[ 2x \frac{dx}{dt} + 2y \frac{dy}{dt} = 0 \implies x \frac{dx}{dt} + y \frac{dy}{dt} = 0 \]

Given \( \frac{dx}{dt} = 2 \) m/min. When \( x = 6 \):

\[ 6^2 + y^2 = 100 \implies y^2 = 64 \implies y = 8 \]

Substitute values:

\[ 6(2) + 8 \frac{dy}{dt} = 0 \] \[ 12 + 8 \frac{dy}{dt} = 0 \] \[ \frac{dy}{dt} = -\frac{12}{8} = -1.5 \text{ m/min} \]

The negative sign indicates the height is decreasing. The rate at which the upper end falls is 1.5 m/min.

A spherical iron ball 10 cm in radius is coated with a layer of ice of uniform thickness that melts at a rate of 50 cm\(^3\)/min. When the thickness of ice is 5 cm, find the rate at which the thickness of ice decreases.

▼

Answer: \( \frac{1}{18\pi} \) cm/min

Let \( x \) be the thickness of the ice. The radius of the iron ball is 10 cm. The total radius of the ball plus ice is \( R = 10 + x \).

Volume of the ice \( V \) is the volume of the outer sphere minus the inner iron sphere:

\[ V = \frac{4}{3}\pi (10+x)^3 - \frac{4}{3}\pi (10)^3 \]

Rate of melting is given as \( \frac{dV}{dt} = -50 \) cm\(^3\)/min.

Differentiating \( V \) w.r.t \( t \):

\[ \frac{dV}{dt} = \frac{4}{3}\pi \cdot 3(10+x)^2 \frac{dx}{dt} = 4\pi (10+x)^2 \frac{dx}{dt} \]

When thickness \( x = 5 \) cm:

\[ -50 = 4\pi (10+5)^2 \frac{dx}{dt} \] \[ -50 = 4\pi (225) \frac{dx}{dt} \] \[ -50 = 900\pi \frac{dx}{dt} \] \[ \frac{dx}{dt} = -\frac{50}{900\pi} = -\frac{1}{18\pi} \]

The rate of decrease is \( \frac{1}{18\pi} \) cm/min.

A stationery company manufactures ‘x’ units of pen in a given time... Cost of raw material is square of pens produced, cost of transportation is twice the number of pens produced and the property tax costs ₹ 5000.
(i) Find the cost function C(x).
(ii) Find the cost of producing 21\(^{\text{st}}\) pen.
(iii) The marginal cost of producing 50 pens.

▼

(i) Cost Function C(x):

Total Cost = Raw Material + Transportation + Tax

\[ C(x) = x^2 + 2x + 5000 \]

(ii) Cost of producing 21\(^{\text{st}}\) pen:

This is the difference between the total cost of 21 pens and 20 pens.

\[ \text{Cost} = C(21) - C(20) \] \[ C(21) = (21)^2 + 2(21) + 5000 = 441 + 42 + 5000 = 5483 \] \[ C(20) = (20)^2 + 2(20) + 5000 = 400 + 40 + 5000 = 5440 \] \[ \text{Cost} = 5483 - 5440 = \text{₹ } 43 \]

(iii) Marginal Cost (MC) of producing 50 pens:

Marginal Cost is the derivative of the Cost function, \( MC(x) = \frac{d}{dx} C(x) \).

\[ MC(x) = 2x + 2 \] \[ \text{At } x = 50, \quad MC(50) = 2(50) + 2 = 100 + 2 = \text{₹ } 102 \]

Q10

A firm knows that the price per unit ‘p’ for one of its product is linear. It also knows that it can sell 1400 units when the price is ₹ 4 per unit, and it can sell 1800 units at a price of ₹ 2 per unit. Find the price per unit if ‘x’ units are sold (or demanded). Also find the revenue function and the marginal revenue function.

▼

1. Demand Function (Price p):

The relationship is linear between \( p \) and \( x \). We have points \( (p_1, x_1) = (4, 1400) \) and \( (p_2, x_2) = (2, 1800) \).

Slope \( m = \frac{x_2 - x_1}{p_2 - p_1} = \frac{1800 - 1400}{2 - 4} = \frac{400}{-2} = -200 \).

Equation of line: \( x - x_1 = m(p - p_1) \)

\[ x - 1400 = -200(p - 4) \] \[ x = -200p + 800 + 1400 \] \[ x = 2200 - 200p \]

Solving for \( p \) in terms of \( x \):

\[ 200p = 2200 - x \implies p = 11 - \frac{x}{200} \]

Or \( p = 11 - 0.005x \).

2. Revenue Function R(x):

\[ R(x) = \text{Price} \times \text{Quantity} = p \cdot x \] \[ R(x) = \left( 11 - \frac{x}{200} \right) x = 11x - \frac{x^2}{200} \]

3. Marginal Revenue Function MR(x):

\[ MR(x) = \frac{d}{dx} R(x) = 11 - \frac{2x}{200} = 11 - \frac{x}{100} \]

Or \( MR(x) = 11 - 0.01x \).

EXERCISE 3.3 (Tangents and Normals) - Deleted from Syllabus

EXERCISE 3.4

Find critical points of the following functions:
i. \( f(x) = x^3 - 6x^2 + 9x - 10 \)
ii. \( f(x) = \frac{\log x}{x}, \quad x > 0 \)
iii. \( f(x) = 50\sqrt{x} - 0.5x - 1000 \)
iv. \( f(x) = 5xe^{-x/3} \)

▼

i. \( f(x) = x^3 - 6x^2 + 9x - 10 \)

Differentiating with respect to \( x \):

\[ f'(x) = 3x^2 - 12x + 9 \]

For critical points, set \( f'(x) = 0 \):

\[ 3(x^2 - 4x + 3) = 0 \] \[ 3(x - 3)(x - 1) = 0 \]

Therefore, critical points are \( x = 1, 3 \).

ii. \( f(x) = \frac{\log x}{x}, \quad x > 0 \)

Using the quotient rule:

\[ f'(x) = \frac{x(\frac{1}{x}) - \log x(1)}{x^2} = \frac{1 - \log x}{x^2} \]

Set \( f'(x) = 0 \):

\[ 1 - \log x = 0 \Rightarrow \log x = 1 \Rightarrow x = e \]

Critical point is \( x = e \).

iii. \( f(x) = 50\sqrt{x} - 0.5x - 1000 \)

\[ f'(x) = 50\left(\frac{1}{2\sqrt{x}}\right) - 0.5 = \frac{25}{\sqrt{x}} - 0.5 \]

Set \( f'(x) = 0 \):

\[ \frac{25}{\sqrt{x}} = 0.5 \Rightarrow \sqrt{x} = \frac{25}{0.5} = 50 \] \[ x = 2500 \]

Critical point is \( x = 2500 \).

iv. \( f(x) = 5xe^{-x/3} \)

Using the product rule:

\[ f'(x) = 5 \left[ 1 \cdot e^{-x/3} + x \cdot e^{-x/3}\left(-\frac{1}{3}\right) \right] \] \[ f'(x) = 5e^{-x/3} \left( 1 - \frac{x}{3} \right) \]

Set \( f'(x) = 0 \):

Since \( e^{-x/3} \neq 0 \), we have \( 1 - \frac{x}{3} = 0 \Rightarrow x = 3 \).

Critical point is \( x = 3 \).

Find the intervals in which the following functions are increasing or decreasing:
i. \( f(x) = x^4 - 8x^3 + 22x^2 - 24x + 1 \)
ii. \( f(x) = (x + 2)^3 (x - 3)^3 \)
iii. \( f(x) = x^2e^x \)

▼

i. \( f(x) = x^4 - 8x^3 + 22x^2 - 24x + 1 \)

\[ f'(x) = 4x^3 - 24x^2 + 44x - 24 = 4(x^3 - 6x^2 + 11x - 6) \]

Factoring the cubic polynomial (Note that \( x=1 \) is a root):

\[ f'(x) = 4(x - 1)(x - 2)(x - 3) \]

Critical points are \( 1, 2, 3 \). We test the intervals:

\( (-\infty, 1) \): \( f'(0) = -24 \) (< 0) \(\Rightarrow\) Decreasing
\( (1, 2) \): \( f'(1.5) > 0 \) \(\Rightarrow\) Increasing
\( (2, 3) \): \( f'(2.5) < 0 \) \(\Rightarrow\) Decreasing
\( (3, \infty) \): \( f'(4) > 0 \) \(\Rightarrow\) Increasing

Increasing: \( (1, 2) \cup (3, \infty) \)
Decreasing: \( (-\infty, 1) \cup (2, 3) \)

ii. \( f(x) = (x + 2)^3 (x - 3)^3 \)

Can be written as \( f(x) = [(x+2)(x-3)]^3 = [x^2 - x - 6]^3 \).

\[ f'(x) = 3[x^2 - x - 6]^2 (2x - 1) \]

Since \( [x^2 - x - 6]^2 \) is always non-negative, the sign depends on \( (2x - 1) \).

\( 2x - 1 > 0 \Rightarrow x > 1/2 \): Increasing
\( 2x - 1 < 0 \Rightarrow x < 1/2 \): Decreasing

Increasing: \( (1/2, \infty) \)
Decreasing: \( (-\infty, 1/2) \)

iii. \( f(x) = x^2e^x \)

\[ f'(x) = 2xe^x + x^2e^x = xe^x(2 + x) \]

Since \( e^x > 0 \), sign depends on \( x(x+2) \). Critical points: \( 0, -2 \).

\( (-\infty, -2) \): \( (-)(-) = (+) \) \(\Rightarrow\) Increasing
\( (-2, 0) \): \( (-)(+) = (-) \) \(\Rightarrow\) Decreasing
\( (0, \infty) \): \( (+)(+) = (+) \) \(\Rightarrow\) Increasing

Increasing: \( (-\infty, -2) \cup (0, \infty) \)
Decreasing: \( (-2, 0) \)

Show that the function \( f(x) = \log(1+x) + \frac{1}{1+x} \) increases on \( (0, \infty) \).

▼

Proof:

Differentiate \( f(x) \):

\[ f'(x) = \frac{1}{1+x} - \frac{1}{(1+x)^2} \] \[ f'(x) = \frac{(1+x) - 1}{(1+x)^2} = \frac{x}{(1+x)^2} \]

For the interval \( (0, \infty) \), we have \( x > 0 \). The denominator \( (1+x)^2 \) is always positive.

Thus, \( f'(x) > 0 \) for all \( x \in (0, \infty) \).

Therefore, the function is strictly increasing on \( (0, \infty) \).

Prove that the function \( f(x) = x^2 - x + 1 \) is neither increasing nor decreasing in \( (0, 1) \).

▼

Proof:

\[ f'(x) = 2x - 1 \]

Set \( f'(x) = 0 \Rightarrow x = 1/2 \).

This critical point divides the interval \( (0, 1) \) into two parts:

In \( (0, 1/2) \): Take \( x = 0.25 \). \( f'(0.25) = 0.5 - 1 = -0.5 < 0 \). (Decreasing)
In \( (1/2, 1) \): Take \( x = 0.75 \). \( f'(0.75) = 1.5 - 1 = 0.5 > 0 \). (Increasing)

Since the function decreases in one part of the interval and increases in the other, it is neither strictly increasing nor strictly decreasing over the entire interval \( (0, 1) \).

A company finds that its total revenue may be determined by \( R(x) = [240000 - (x-500)^2] \). Find when is the revenue function increasing and when decreasing?

▼

Answer: Increasing in \( [0, 500) \), Decreasing in \( (500, \infty) \)

Given \( R(x) = 240000 - (x-500)^2 \).

\[ R'(x) = 0 - 2(x-500)(1) = 2(500 - x) \]

Increasing: \( R'(x) > 0 \Rightarrow 2(500 - x) > 0 \Rightarrow 500 > x \Rightarrow x < 500 \).
Since units sold \( x \) cannot be negative, interval is \( [0, 500) \).
Decreasing: \( R'(x) < 0 \Rightarrow 2(500 - x) < 0 \Rightarrow 500 < x \Rightarrow x > 500 \).

The price 'p' per unit is given by the relation \( x = \frac{1}{3}p^2 - 2p + 3 \) where 'x' is the number of units sold then,
i. Find the revenue function R.
ii. Find the price interval for which the revenue is increasing and decreasing.

▼

i. Revenue Function R

Revenue \( R = \text{Price} \times \text{Quantity} = p \cdot x \).

Substituting the value of \( x \):

\[ R(p) = p \left( \frac{1}{3}p^2 - 2p + 3 \right) = \frac{1}{3}p^3 - 2p^2 + 3p \]

ii. Intervals for Revenue

Differentiating \( R \) with respect to \( p \):

\[ \frac{dR}{dp} = p^2 - 4p + 3 \]

Set \( \frac{dR}{dp} = 0 \):

\[ p^2 - 4p + 3 = 0 \Rightarrow (p - 3)(p - 1) = 0 \]

Critical points are \( p = 1, 3 \).

In \( (0, 1) \): \( R' > 0 \) (Increasing)
In \( (1, 3) \): \( R' < 0 \) (Decreasing)
In \( (3, \infty) \): \( R' > 0 \) (Increasing)

Revenue is Increasing: For \( p \in (0, 1) \cup (3, \infty) \).
Revenue is Decreasing: For \( p \in (1, 3) \).

The total cost function of a manufacturing company is given by \( C(x) = 2x\left(\frac{x+4}{x+3}\right) + 3 \). Show that MC (Marginal Cost) falls continuously as the output 'x' increases.

▼

Proof:

First simplify \( C(x) \):

\[ C(x) = 2 \left( \frac{x^2+4x}{x+3} \right) + 3 = 2 \left( \frac{x(x+3) + x}{x+3} \right) + 3 \] \[ = 2 \left( x + \frac{x}{x+3} \right) + 3 = 2x + \frac{2x}{x+3} + 3 \] \[ = 2x + \frac{2(x+3) - 6}{x+3} + 3 = 2x + 2 - \frac{6}{x+3} + 3 = 2x + 5 - \frac{6}{x+3} \]

Find Marginal Cost (MC) by differentiating \( C(x) \):

\[ MC = \frac{d}{dx} \left( 2x + 5 - 6(x+3)^{-1} \right) \] \[ MC = 2 + 0 - 6(-1)(x+3)^{-2} = 2 + \frac{6}{(x+3)^2} \]

To check if MC falls, we find the rate of change of MC with respect to \( x \):

\[ \frac{d}{dx}(MC) = \frac{d}{dx} \left( 2 + 6(x+3)^{-2} \right) \] \[ = -12(x+3)^{-3} = \frac{-12}{(x+3)^3} \]

For any output \( x > 0 \), the term \( (x+3)^3 \) is positive. Therefore, \( \frac{d}{dx}(MC) \) is always negative.

This implies that the Marginal Cost falls continuously as output increases.

The price 'p' per unit at which a company can sell all that it produces is given by \( p = 29 - x \), where 'x' is the number of units produced. The total cost function \( C(x) = 45 + 11x \). If \( P(x) = R(x) - C(x) \), is the profit function then find the interval in which the profit is increasing and decreasing.

▼

Answer: Increasing in \( (0, 9) \), Decreasing in \( (9, \infty) \)

1. Revenue Function R(x):

\[ R(x) = p \cdot x = (29 - x)x = 29x - x^2 \]

2. Profit Function P(x):

\[ P(x) = R(x) - C(x) = (29x - x^2) - (45 + 11x) \] \[ P(x) = -x^2 + 18x - 45 \]

3. Intervals:

\[ P'(x) = -2x + 18 \]

Increasing: \( P'(x) > 0 \Rightarrow -2x + 18 > 0 \Rightarrow 18 > 2x \Rightarrow x < 9 \). Interval: \( (0, 9) \).
Decreasing: \( P'(x) < 0 \Rightarrow -2x + 18 < 0 \Rightarrow 18 < 2x \Rightarrow x > 9 \). Interval: \( (9, \infty) \).

EXERCISE 3.5

Find the local maxima, local minima, local minimum value and local maximum value, if any of the following:
i. \( f(x) = x^2 - 6x + 16 \)
ii. \( f(x) = \frac{\log x}{x}, \quad x > 0 \)
iii. \( f(x) = (1-x^2)e^x \)
iv. \( f(x) = \frac{x^2 - 7x + 6}{x - 10} \)
v. \( f(x) = 2x + \frac{1}{2x} \)

▼

i. \( f(x) = x^2 - 6x + 16 \)

\[ f'(x) = 2x - 6 \]

Set \( f'(x) = 0 \Rightarrow 2x = 6 \Rightarrow x = 3 \).

\[ f''(x) = 2 > 0 \]

Since \( f''(3) > 0 \), \( x = 3 \) is a point of local minima.

Local Minimum Value: \( f(3) = 3^2 - 6(3) + 16 = 9 - 18 + 16 = 7 \).

ii. \( f(x) = \frac{\log x}{x} \)

\[ f'(x) = \frac{x(1/x) - \log x(1)}{x^2} = \frac{1 - \log x}{x^2} \]

Set \( f'(x) = 0 \Rightarrow 1 - \log x = 0 \Rightarrow \log x = 1 \Rightarrow x = e \).

\[ f''(x) = \frac{x^2(-1/x) - (1-\log x)(2x)}{x^4} = \frac{-x - 2x(1-\log x)}{x^4} \]

At \( x = e \): \( f''(e) = \frac{-e - 0}{e^4} < 0 \). Maxima.

Local Maximum Value: \( f(e) = \frac{1}{e} \).

iii. \( f(x) = (1-x^2)e^x \)

\[ f'(x) = (1-x^2)e^x + e^x(-2x) = e^x(1 - x^2 - 2x) \]

Set \( f'(x) = 0 \Rightarrow x^2 + 2x - 1 = 0 \).

Roots: \( x = \frac{-2 \pm \sqrt{4+4}}{2} = -1 \pm \sqrt{2} \).

Let \( \alpha = -1-\sqrt{2} \) and \( \beta = -1+\sqrt{2} \).

Using the first derivative test or checking signs, \( x = -1+\sqrt{2} \) is a maximum and \( x = -1-\sqrt{2} \) is a minimum.

iv. \( f(x) = \frac{x^2 - 7x + 6}{x - 10} \)

\[ f'(x) = \frac{(x-10)(2x-7) - (x^2-7x+6)(1)}{(x-10)^2} \] \[ f'(x) = \frac{2x^2 - 27x + 70 - x^2 + 7x - 6}{(x-10)^2} = \frac{x^2 - 20x + 64}{(x-10)^2} \]

Set \( f'(x) = 0 \Rightarrow x^2 - 20x + 64 = 0 \Rightarrow (x-16)(x-4) = 0 \).

Critical points: \( x = 4, 16 \).

At \( x=4 \): Maxima (Value = \( \frac{16-28+6}{4-10} = \frac{-6}{-6} = 1 \))
At \( x=16 \): Minima (Value = \( \frac{256-112+6}{16-10} = \frac{150}{6} = 25 \))

v. \( f(x) = 2x + \frac{1}{2x} \)

\[ f'(x) = 2 - \frac{1}{2x^2} \]

Set \( f'(x) = 0 \Rightarrow 4x^2 = 1 \Rightarrow x = \pm \frac{1}{2} \).

\[ f''(x) = \frac{1}{x^3} \]

At \( x = 1/2 \), \( f'' > 0 \) (Minima). Value = \( 1 + 1 = 2 \).
At \( x = -1/2 \), \( f'' < 0 \) (Maxima). Value = \( -1 - 1 = -2 \).

The sum of two positive numbers is 16. Find the numbers, if the product of the squares is to be maximum.
(Note: Assuming the question implies "product of the squares of the numbers" or "sum of squares"? Standard text usually asks for sum of squares or product of one square and other cube. Based on text "product of the squares", we maximize \( x^2 y^2 \).)

▼

Answer: 8, 8

Let numbers be \( x \) and \( y \). Given \( x + y = 16 \Rightarrow y = 16 - x \).

Let Product \( P = x^2 y^2 = (xy)^2 \).

To maximize \( P \), we can maximize \( Z = xy \) (since square function is increasing for positive numbers).

\[ Z = x(16 - x) = 16x - x^2 \] \[ \frac{dZ}{dx} = 16 - 2x \]

Set \( \frac{dZ}{dx} = 0 \Rightarrow 2x = 16 \Rightarrow x = 8 \).

Then \( y = 16 - 8 = 8 \).

Checking second derivative: \( \frac{d^2Z}{dx^2} = -2 < 0 \) (Maxima).

The numbers are 8 and 8.

Show that of all rectangles with a given perimeter, the square has the largest area.

▼

Proof:

Let perimeter be \( P \) (constant) and sides be \( x \) and \( y \).

\[ 2(x + y) = P \Rightarrow y = \frac{P}{2} - x \]

Area \( A = xy = x(\frac{P}{2} - x) = \frac{P}{2}x - x^2 \).

Differentiate w.r.t \( x \):

\[ \frac{dA}{dx} = \frac{P}{2} - 2x \]

Set to 0 for critical point: \( 2x = \frac{P}{2} \Rightarrow x = \frac{P}{4} \).

Then \( y = \frac{P}{2} - \frac{P}{4} = \frac{P}{4} \).

Since \( x = y \), the rectangle is a square.

Second derivative \( \frac{d^2A}{dx^2} = -2 < 0 \), confirming maximum area.

Show that the function \( f(x) = x^3 - 6x^2 + 12x + 50 \) has neither a local maximum nor a local minimum value.

▼

Proof:

Find the derivative:

\[ f'(x) = 3x^2 - 12x + 12 \] \[ f'(x) = 3(x^2 - 4x + 4) \] \[ f'(x) = 3(x - 2)^2 \]

The critical point is \( x = 2 \).

However, \( f'(x) \) is always non-negative ( \( \geq 0 \) ) for all real \( x \). The sign of the derivative does not change as \( x \) passes through 2 (it stays positive).

Therefore, \( x = 2 \) is a point of inflection, not a maxima or minima.

The profit function, in rupees, of a firm selling 'x' items (\( x \geq 0 \)) per week is given by \( P(x) = (400 - x)x - 3500 \). How many items should the firm sell to make the maximum profit? Also find the maximum profit.

▼

Answer: 200 items; Max Profit ₹ 36,500

\[ P(x) = 400x - x^2 - 3500 \]

Differentiate w.r.t \( x \):

\[ P'(x) = 400 - 2x \]

Set \( P'(x) = 0 \):

\[ 400 - 2x = 0 \Rightarrow 2x = 400 \Rightarrow x = 200 \]

Check second derivative:

\[ P''(x) = -2 < 0 \quad (\text{Maxima}) \]

Maximum Profit:

\[ P(200) = (400 - 200)(200) - 3500 \] \[ = 200 \times 200 - 3500 \] \[ = 40000 - 3500 = 36500 \]

A tour operator charges ₹ 136 per passenger for 100 passengers with a discount of ₹ 4 for each 10 passengers in excess of 100. Find the number of passengers that will maximise the amount of money the tour operator receives.

▼

Answer: 120 passengers

Let \( x \) be the number of passengers in excess of 100.

Total passengers = \( 100 + x \).

Discount calculation: Discount is ₹ 4 for every 10 excess passengers. Discount per passenger = \( \frac{4}{10}x = 0.4x \).

New Price per passenger = \( 136 - 0.4x \).

Total Revenue \( R(x) = (\text{Price}) \times (\text{Quantity}) \):

\[ R(x) = (136 - 0.4x)(100 + x) \] \[ R(x) = 13600 + 136x - 40x - 0.4x^2 \] \[ R(x) = 13600 + 96x - 0.4x^2 \]

Differentiate w.r.t \( x \):

\[ R'(x) = 96 - 0.8x \]

Set \( R'(x) = 0 \):

\[ 0.8x = 96 \Rightarrow x = \frac{960}{8} = 120 \]

Excess passengers = 120. (Check \( R''(x) = -0.8 < 0 \) Maxima).

Total passengers = \( 100 + 120 = 220 \).

Note: Sometimes this problem is interpreted as "Discount of ₹ 4 is applied to the *entire* group for *each* batch of 10 excess". However, the standard calculus interpretation (continuous variable) is used here. If interpreted strictly as batches of 10, \( x \) would be batches. Let's assume \( x \) is the count of excess passengers and discount is continuous.

Correction: Let's re-read carefully: "discount of ₹ 4 for each 10 passengers in excess".

Alternative interpretation: Let \( n \) be the number of 10-passenger batches. \( n = \frac{excess}{10} \). Discount = \( 4n \). Price = \( 136 - 4n \). Total = \( (100 + 10n)(136 - 4n) \). Maximizing this yields same result structure.

Wait, if \( x = 120 \), Price = \( 136 - 0.4(120) = 136 - 48 = 88 \). Rev = \( 220 \times 88 = 19360 \). (At \( x=0 \), Rev=13600).

So, the number of passengers is 220.

If price 'p' per unit of an article is \( p = 75 - 2x \) and the cost function is \( C(x) = 350 + 12x + \frac{x^2}{4} \). Find the number of units and the price at which the total profit is maximum. What is the maximum profit?

▼

Answer: Units = 14, Price = 47, Profit = 91

Revenue \( R(x) = p \cdot x = (75 - 2x)x = 75x - 2x^2 \).

Profit \( P(x) = R(x) - C(x) \):

\[ P(x) = (75x - 2x^2) - \left( 350 + 12x + \frac{x^2}{4} \right) \] \[ P(x) = 63x - 2x^2 - 0.25x^2 - 350 \] \[ P(x) = 63x - 2.25x^2 - 350 \]

Differentiate:

\[ P'(x) = 63 - 4.5x \]

Set \( P'(x) = 0 \):

\[ 4.5x = 63 \Rightarrow x = \frac{63}{4.5} = \frac{630}{45} = 14 \]

Number of units = 14.

Price \( p = 75 - 2(14) = 75 - 28 = 47 \).

Max Profit:

\[ P(14) = 63(14) - 2.25(14^2) - 350 \] \[ = 882 - 2.25(196) - 350 \] \[ = 882 - 441 - 350 = 91 \]

The cost of fuel in running an engine is proportional to the square of the speed in kms per hour, and is ₹ 48 per hour when the speed is 16 km. Other costs amount to ₹ 300 per hour. Find the most economical speed.

▼

Answer: 40 km/hr

Let speed be \( v \) km/hr. Fuel cost per hour \( C_f = k v^2 \).

Given: \( 48 = k(16)^2 \Rightarrow 48 = 256k \Rightarrow k = \frac{48}{256} = \frac{3}{16} \).

So, fuel cost per hour = \( \frac{3}{16}v^2 \).

Total cost per hour \( C_h = \frac{3}{16}v^2 + 300 \).

To find the "most economical speed", we must minimize the Cost per kilometer (not per hour).

Cost per km \( C = \frac{\text{Cost per hour}}{\text{Speed}} = \frac{\frac{3}{16}v^2 + 300}{v} \).

\[ C(v) = \frac{3}{16}v + \frac{300}{v} \]

Differentiate w.r.t \( v \):

\[ C'(v) = \frac{3}{16} - \frac{300}{v^2} \]

Set \( C'(v) = 0 \):

\[ \frac{3}{16} = \frac{300}{v^2} \] \[ 3v^2 = 4800 \Rightarrow v^2 = 1600 \Rightarrow v = 40 \text{ km/hr} \]

CASE BASED QUESTIONS

Case Study-I

Context: A farmer has a piece of land. He observed that he got 600 units of fruits per tree by planting upto 25 trees and when 26 trees were grown, he received 15210 units of fruits, for 27 trees he ended up with 15390 fruits, for 28 trees he got 15540 fruits and this sequence of production of fruits continues in the same pattern as more trees, in excess of 25, were grown.

If ‘x’ more trees, in excess of 25 are grown, then the number of fruits produced per tree is:
i. \( 600 - 15x \) ii. \( 600 + 15x \) iii. \( 600x - 15 \) iv. \( 600x + 15 \)

▼

Answer: i. \( 600 - 15x \)

The base production is 600 fruits. We calculate the decrease per tree based on the data:

For 26 trees (1 excess), total = 15210. Yield/tree = \( 15210/26 = 585 \). Decrease = \( 600 - 585 = 15 \).
For 27 trees (2 excess), total = 15390. Yield/tree = \( 15390/27 = 570 \). Decrease = \( 585 - 570 = 15 \).

The yield decreases by 15 for every excess tree \( x \). So, Yield = \( 600 - 15x \).

The production of entire garden if ‘x’ more trees, in excess of 25, are planted:
i. \( (25 + x)(600 + 15x) \) ii. \( (25 - x)(600 - 15x) \)
iii. \( (25 + x)(600 - 15x) \) iv. \( (25 + x)(15x - 600) \)

▼

Answer: iii. \( (25 + x)(600 - 15x) \)

Total Production = (Total Trees) \(\times\) (Yield per Tree).

Total Trees = \( 25 + x \)
Yield per Tree = \( 600 - 15x \)

\[ P(x) = (25 + x)(600 - 15x) \]

The marginal production of the garden when ‘x’ more trees, in excess of 25, are planted:
i. \( 225 + 30x \) ii. \( 225 - 30x \) iii. \( 225x + 30 \) iv. \( 225x - 30 \)

▼

Answer: ii. \( 225 - 30x \)

Expand the production function \( P(x) \):

\[ P(x) = (25 + x)(600 - 15x) = 15000 - 375x + 600x - 15x^2 \] \[ P(x) = 15000 + 225x - 15x^2 \]

Marginal production \( P'(x) \):

\[ P'(x) = 225 - 30x \]

The critical point of producing ‘x’ more units of trees is:
i. 7 ii. 8 iii. 7.5 iv. 8.5

▼

Answer: iii. 7.5

Set Marginal Production to 0:

\[ 225 - 30x = 0 \Rightarrow 30x = 225 \Rightarrow x = 7.5 \]

The number of trees to be grown to get maximum production is:
i. 30 or 31 trees ii. 32 or 33 trees iii. 33 or 34 trees iv. 34 or 35 trees

▼

Answer: ii. 32 or 33 trees

Critical point \( x = 7.5 \). Integers close to 7.5 are 7 and 8.

For \( x=7 \): Trees = \( 25+7 = 32 \).
For \( x=8 \): Trees = \( 25+8 = 33 \).

Case Study-II

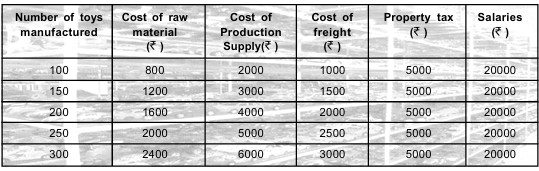
Context: A manufacturing company manufactures toys, the company observed the following costs at different production levels (as shown in the table above).

Which of the following is the fixed cost
i. Number of toys manufactured ii. Cost of raw material
iii. Cost of production supply iv. Salaries

▼

Answer: iv. Salaries

In the table, "Salaries" remain constant (₹ 20000) regardless of the number of toys manufactured.

Total cost \( C(x) \) of toys for ‘x’ units of production is
i. \( C(x) = 8x^2 + 30x + 25000 \) ii. \( C(x) = 8x^2 + 30x + 20000 \)
iii. \( C(x) = 38x + 25000 \) iv. \( C(x) = 28x + 25000 \)

▼

Answer: iii. \( C(x) = 38x + 25000 \)

Variable Cost per unit (calculated from 100 units):

Raw Material: 800/100 = 8
Production Supply: 2000/100 = 20
Freight: 1000/100 = 10
Total Variable = \( 8 + 20 + 10 = 38 \)

Fixed Cost: Tax (5000) + Salaries (20000) = 25000.

\[ C(x) = 38x + 25000 \]

If the company observes the price ‘p’ per unit of item sold \( p = 5000 - 10x \), where ‘x’ is the number of units sold. Then the revenue function R(x) is given by,
i. \( R(x) = 5000x - 10x^2 \) ii. \( R(p) = 5000p - 10p^2 \)
iii. \( R(x) = 5000 - 10x^2 \) iv. \( R(p) = 5000 - 10p^2 \)

▼

Answer: i. \( R(x) = 5000x - 10x^2 \)

\[ R(x) = \text{Price} \times \text{Quantity} = (5000 - 10x)x = 5000x - 10x^2 \]

The Marginal revenue (MR) of the company is given by
i. \( 5000 - 20x \) ii. \( 5000 - 20p \)
iii. \( -20x \) iv. \( -20p \)

▼

Answer: i. \( 5000 - 20x \)

\[ MR = \frac{d}{dx} R(x) = \frac{d}{dx}(5000x - 10x^2) = 5000 - 20x \]

If the profit function \( P(x) = R(x) - C(x) \), then it is given by
i. \( -18x^2 + 4970x - 25000 \) ii. \( -10x^2 + 4962x - 20000 \)
iii. \( 10x^2 + 4962x - 25000 \) iv. \( -10x^2 + 4962x - 25000 \)

▼

Answer: iv. \( -10x^2 + 4962x - 25000 \)

\[ P(x) = (5000x - 10x^2) - (38x + 25000) \] \[ P(x) = -10x^2 + (5000 - 38)x - 25000 \] \[ P(x) = -10x^2 + 4962x - 25000 \]