NCERT Solutions Class-12-Chapter-10-Vector Algebra
Excercise-10.1
Note:
Scalars vs Vectors: Scalars have magnitude only (e.g., mass, distance). Vectors have magnitude and direction (e.g., displacement, force).
Vector Types:
- Coinitial: Start from the same point.
- Equal: Same magnitude and direction.
- Collinear: Parallel to the same line (direction can be same or opposite).
Q1
Represent graphically a displacement of 40 km, 30° east of north.▼
Solution:
To represent this vector:
- Draw the North-South and East-West axes.
- Measure an angle of 30° towards the East from the North axis.
- Draw a vector of length corresponding to 40 km (e.g., 4 units) along this line.
Q2
Classify the following measures as scalars and vectors.
(i) 10 kg
(ii) 2 meters north-west
(iii) 40°
(iv) 40 watt
(v) \( 10^{-19} \) coulomb
(vi) \( 20 \text{ m/s}^2 \)▼
(i) 10 kg
(ii) 2 meters north-west
(iii) 40°
(iv) 40 watt
(v) \( 10^{-19} \) coulomb
(vi) \( 20 \text{ m/s}^2 \)
Solution:
- (i) Scalar: Mass (magnitude only).
- (ii) Vector: Displacement (magnitude + direction).
- (iii) Scalar: Angle (magnitude).
- (iv) Scalar: Power (magnitude only).
- (v) Scalar: Charge (magnitude only).
- (vi) Vector: Acceleration (magnitude + direction).
Q3
Classify the following as scalar and vector quantities.
(i) time period
(ii) distance
(iii) force
(iv) velocity
(v) work done▼
(i) time period
(ii) distance
(iii) force
(iv) velocity
(v) work done
Solution:
- (i) Scalar: Time.
- (ii) Scalar: Distance (path length).
- (iii) Vector: Force.
- (iv) Vector: Velocity.
- (v) Scalar: Work done.
Q4
In Fig 10.6 (a square), identify the following vectors.▼
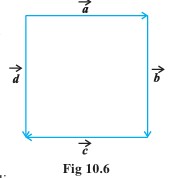
(i) Coinitial
(ii) Equal
(iii) Collinear but not equal
Solution:
- (i) Coinitial: Vectors starting from the same point.
From the figure, \( \vec{a} \) and \( \vec{d} \) start from the same vertex.
Ans: \( \vec{a} \) and \( \vec{d} \). - (ii) Equal: Vectors with same magnitude and direction.
From the figure, \( \vec{d} \) and \( \vec{b} \) correspond to opposite sides of the square and point in the same direction.
Ans: \( \vec{d} \) and \( \vec{b} \). - (iii) Collinear but not equal: Parallel vectors with different directions.
\( \vec{a} \) and \( \vec{c} \) are parallel but point in opposite directions.
Ans: \( \vec{a} \) and \( \vec{c} \).
Q5
Answer the following as true or false.
(i) \( \vec{a} \) and \( -\vec{a} \) are collinear.
(ii) Two collinear vectors are always equal in magnitude.
(iii) Two vectors having same magnitude are collinear.
(iv) Two collinear vectors having the same magnitude are equal.▼
(i) \( \vec{a} \) and \( -\vec{a} \) are collinear.
(ii) Two collinear vectors are always equal in magnitude.
(iii) Two vectors having same magnitude are collinear.
(iv) Two collinear vectors having the same magnitude are equal.
Solution:
- (i) True: They are parallel (antiparallel).
- (ii) False: Collinear means parallel; magnitude can differ.
- (iii) False: Same magnitude doesn't imply parallel direction.
- (iv) False: They could be opposite in direction (e.g., \( \vec{a} \) and \( -\vec{a} \)).
