NCERT Solutions Class-12-Chapter-10-Vector Algebra
Excercise-10.2
Note:
Magnitude of a vector \( \vec{a} = x\hat{i} + y\hat{j} + z\hat{k} \) is \( |\vec{a}| = \sqrt{x^2 + y^2 + z^2} \).
Unit Vector: \( \hat{a} = \frac{\vec{a}}{|\vec{a}|} \).
Vector joining two points \( P(x_1, y_1, z_1) \) and \( Q(x_2, y_2, z_2) \) is \( \vec{PQ} = (x_2-x_1)\hat{i} + (y_2-y_1)\hat{j} + (z_2-z_1)\hat{k} \).
Section Formula: Position vector of point \( R \) dividing \( PQ \) in ratio \( m:n \) is \( \vec{r} = \frac{m\vec{b} + n\vec{a}}{m+n} \) (internal) and \( \vec{r} = \frac{m\vec{b} - n\vec{a}}{m-n} \) (external).
Q1
Compute the magnitude of the following vectors:
\( \vec{a} = \hat{i} + \hat{j} + \hat{k} \); \( \vec{b} = 2\hat{i} - 7\hat{j} - 3\hat{k} \); \( \vec{c} = \frac{1}{\sqrt{3}}\hat{i} + \frac{1}{\sqrt{3}}\hat{j} - \frac{1}{\sqrt{3}}\hat{k} \)▼
\( \vec{a} = \hat{i} + \hat{j} + \hat{k} \); \( \vec{b} = 2\hat{i} - 7\hat{j} - 3\hat{k} \); \( \vec{c} = \frac{1}{\sqrt{3}}\hat{i} + \frac{1}{\sqrt{3}}\hat{j} - \frac{1}{\sqrt{3}}\hat{k} \)
Solution:
For \( \vec{a} \): \( |\vec{a}| = \sqrt{1^2 + 1^2 + 1^2} = \sqrt{3} \).
For \( \vec{b} \): \( |\vec{b}| = \sqrt{2^2 + (-7)^2 + (-3)^2} = \sqrt{4 + 49 + 9} = \sqrt{62} \).
For \( \vec{c} \): \( |\vec{c}| = \sqrt{(\frac{1}{\sqrt{3}})^2 + (\frac{1}{\sqrt{3}})^2 + (-\frac{1}{\sqrt{3}})^2} = \sqrt{\frac{1}{3} + \frac{1}{3} + \frac{1}{3}} = \sqrt{1} = 1 \).
Q2
Write two different vectors having same magnitude.▼
Solution:
Let \( \vec{a} = \hat{i} + 2\hat{j} + 3\hat{k} \). Magnitude \( |\vec{a}| = \sqrt{1+4+9} = \sqrt{14} \).
Let \( \vec{b} = 2\hat{i} + \hat{j} + 3\hat{k} \). Magnitude \( |\vec{b}| = \sqrt{4+1+9} = \sqrt{14} \).
Here, \( \vec{a} \neq \vec{b} \) but \( |\vec{a}| = |\vec{b}| \).
Q3
Write two different vectors having same direction.▼
Solution:
Let \( \vec{a} = \hat{i} + \hat{j} + \hat{k} \).
Let \( \vec{b} = 2(\hat{i} + \hat{j} + \hat{k}) = 2\hat{i} + 2\hat{j} + 2\hat{k} \).
Since direction cosines of both vectors are same \( (\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}) \), they have the same direction but different magnitudes.
Q4
Find the values of \( x \) and \( y \) so that the vectors \( 2\hat{i} + 3\hat{j} \) and \( x\hat{i} + y\hat{j} \) are equal.▼
Solution:
Two vectors are equal if their corresponding scalar components are equal.
\( 2\hat{i} + 3\hat{j} = x\hat{i} + y\hat{j} \).
Comparing coefficients: \( x = 2 \) and \( y = 3 \).
Q5
Find the scalar and vector components of the vector with initial point \( (2, 1) \) and terminal point \( (-5, 7) \).▼
Solution:
Let \( P(2, 1) \) and \( Q(-5, 7) \).
\( \vec{PQ} = (-5 - 2)\hat{i} + (7 - 1)\hat{j} = -7\hat{i} + 6\hat{j} \).
Scalar components: -7 and 6.
Vector components: \( -7\hat{i} \) and \( 6\hat{j} \).
Q6
Find the sum of the vectors \( \vec{a} = \hat{i} - 2\hat{j} + \hat{k} \), \( \vec{b} = -2\hat{i} + 4\hat{j} + 5\hat{k} \) and \( \vec{c} = \hat{i} - 6\hat{j} - 7\hat{k} \).▼
Solution:
\( \vec{a} + \vec{b} + \vec{c} = (1 - 2 + 1)\hat{i} + (-2 + 4 - 6)\hat{j} + (1 + 5 - 7)\hat{k} \).
\( = 0\hat{i} - 4\hat{j} - 1\hat{k} = -4\hat{j} - \hat{k} \).
Q7
Find the unit vector in the direction of the vector \( \vec{a} = \hat{i} + \hat{j} + 2\hat{k} \).▼
Solution:
\( |\vec{a}| = \sqrt{1^2 + 1^2 + 2^2} = \sqrt{1+1+4} = \sqrt{6} \).
Unit vector \( \hat{a} = \frac{\vec{a}}{|\vec{a}|} = \frac{1}{\sqrt{6}}\hat{i} + \frac{1}{\sqrt{6}}\hat{j} + \frac{2}{\sqrt{6}}\hat{k} \).
Q8
Find the unit vector in the direction of vector \( \vec{PQ} \), where P and Q are the points \( (1, 2, 3) \) and \( (4, 5, 6) \), respectively.▼
Solution:
\( \vec{PQ} = (4-1)\hat{i} + (5-2)\hat{j} + (6-3)\hat{k} = 3\hat{i} + 3\hat{j} + 3\hat{k} \).
\( |\vec{PQ}| = \sqrt{3^2 + 3^2 + 3^2} = \sqrt{27} = 3\sqrt{3} \).
Unit vector = \( \frac{3\hat{i} + 3\hat{j} + 3\hat{k}}{3\sqrt{3}} = \frac{1}{\sqrt{3}}\hat{i} + \frac{1}{\sqrt{3}}\hat{j} + \frac{1}{\sqrt{3}}\hat{k} \).
Q9
For given vectors, \( \vec{a} = 2\hat{i} - \hat{j} + 2\hat{k} \) and \( \vec{b} = -\hat{i} + \hat{j} - \hat{k} \), find the unit vector in the direction of the vector \( \vec{a} + \vec{b} \).▼
Solution:
Let \( \vec{c} = \vec{a} + \vec{b} = (2-1)\hat{i} + (-1+1)\hat{j} + (2-1)\hat{k} = \hat{i} + \hat{k} \).
\( |\vec{c}| = \sqrt{1^2 + 1^2} = \sqrt{2} \).
Unit vector \( \hat{c} = \frac{1}{\sqrt{2}}\hat{i} + \frac{1}{\sqrt{2}}\hat{k} \).
Q10
Find a vector in the direction of vector \( 5\hat{i} - \hat{j} + 2\hat{k} \) which has magnitude 8 units.▼
Solution:
Let \( \vec{a} = 5\hat{i} - \hat{j} + 2\hat{k} \).
\( |\vec{a}| = \sqrt{25 + 1 + 4} = \sqrt{30} \).
Unit vector \( \hat{a} = \frac{1}{\sqrt{30}}(5\hat{i} - \hat{j} + 2\hat{k}) \).
Required vector = \( 8 \hat{a} = \frac{8}{\sqrt{30}}(5\hat{i} - \hat{j} + 2\hat{k}) = \frac{40}{\sqrt{30}}\hat{i} - \frac{8}{\sqrt{30}}\hat{j} + \frac{16}{\sqrt{30}}\hat{k} \).
Q11
Show that the vectors \( 2\hat{i} - 3\hat{j} + 4\hat{k} \) and \( -4\hat{i} + 6\hat{j} - 8\hat{k} \) are collinear.▼
Solution:
Let \( \vec{a} = 2\hat{i} - 3\hat{j} + 4\hat{k} \).
Let \( \vec{b} = -4\hat{i} + 6\hat{j} - 8\hat{k} = -2(2\hat{i} - 3\hat{j} + 4\hat{k}) \).
So, \( \vec{b} = -2\vec{a} \).
Since \( \vec{b} = \lambda \vec{a} \) (where \( \lambda = -2 \)), the vectors are collinear.
Q12
Find the direction cosines of the vector \( \hat{i} + 2\hat{j} + 3\hat{k} \).▼
Solution:
Let \( \vec{a} = \hat{i} + 2\hat{j} + 3\hat{k} \).
Magnitude \( |\vec{a}| = \sqrt{1^2 + 2^2 + 3^2} = \sqrt{1+4+9} = \sqrt{14} \).
Direction cosines are \( \frac{1}{\sqrt{14}}, \frac{2}{\sqrt{14}}, \frac{3}{\sqrt{14}} \).
Q13
Find the direction cosines of the vector joining the points \( A(1, 2, -3) \) and \( B(-1, -2, 1) \), directed from A to B.▼
Solution:
\( \vec{AB} = (-1-1)\hat{i} + (-2-2)\hat{j} + (1-(-3))\hat{k} = -2\hat{i} - 4\hat{j} + 4\hat{k} \).
Magnitude \( |\vec{AB}| = \sqrt{(-2)^2 + (-4)^2 + 4^2} = \sqrt{4 + 16 + 16} = \sqrt{36} = 6 \).
Direction cosines: \( \frac{-2}{6}, \frac{-4}{6}, \frac{4}{6} \Rightarrow -\frac{1}{3}, -\frac{2}{3}, \frac{2}{3} \).
Q14
Show that the vector \( \hat{i} + \hat{j} + \hat{k} \) is equally inclined to the axes OX, OY and OZ.▼
Solution:
Let \( \vec{a} = \hat{i} + \hat{j} + \hat{k} \). Magnitude \( |\vec{a}| = \sqrt{3} \).
Direction cosines are: \( \cos \alpha = \frac{1}{\sqrt{3}}, \cos \beta = \frac{1}{\sqrt{3}}, \cos \gamma = \frac{1}{\sqrt{3}} \).
Since \( \cos \alpha = \cos \beta = \cos \gamma \), the angles \( \alpha, \beta, \gamma \) are equal.
Hence, the vector is equally inclined to the axes.
Q15
Find the position vector of a point R which divides the line joining two points P and Q whose position vectors are \( \hat{i} + 2\hat{j} - \hat{k} \) and \( -\hat{i} + \hat{j} + \hat{k} \) respectively, in the ratio 2 : 1
(i) internally
(ii) externally▼
(i) internally
(ii) externally
Solution:
Let \( \vec{a} = \hat{i} + 2\hat{j} - \hat{k} \) and \( \vec{b} = -\hat{i} + \hat{j} + \hat{k} \). Ratio \( m:n = 2:1 \).
(i) Internally:
\( \vec{r} = \frac{m\vec{b} + n\vec{a}}{m+n} = \frac{2(-\hat{i} + \hat{j} + \hat{k}) + 1(\hat{i} + 2\hat{j} - \hat{k})}{2+1} \).
\( = \frac{-2\hat{i} + 2\hat{j} + 2\hat{k} + \hat{i} + 2\hat{j} - \hat{k}}{3} = \frac{-\hat{i} + 4\hat{j} + \hat{k}}{3} \).
\( \vec{r} = -\frac{1}{3}\hat{i} + \frac{4}{3}\hat{j} + \frac{1}{3}\hat{k} \).
(ii) Externally:
\( \vec{r} = \frac{m\vec{b} - n\vec{a}}{m-n} = \frac{2(-\hat{i} + \hat{j} + \hat{k}) - 1(\hat{i} + 2\hat{j} - \hat{k})}{2-1} \).
\( = -2\hat{i} + 2\hat{j} + 2\hat{k} - \hat{i} - 2\hat{j} + \hat{k} = -3\hat{i} + 3\hat{k} \).
Q16
Find the position vector of the mid point of the vector joining the points \( P(2, 3, 4) \) and \( Q(4, 1, -2) \).▼
Solution:
Mid-point formula: \( \frac{\vec{a} + \vec{b}}{2} \).
\( \vec{p} = 2\hat{i} + 3\hat{j} + 4\hat{k} \); \( \vec{q} = 4\hat{i} + \hat{j} - 2\hat{k} \).
Mid-point vector \( = \frac{(2+4)\hat{i} + (3+1)\hat{j} + (4-2)\hat{k}}{2} = \frac{6\hat{i} + 4\hat{j} + 2\hat{k}}{2} = 3\hat{i} + 2\hat{j} + \hat{k} \).
Q17
Show that the points A, B and C with position vectors, \( \vec{a} = 3\hat{i} - 4\hat{j} - 4\hat{k} \), \( \vec{b} = 2\hat{i} - \hat{j} + \hat{k} \) and \( \vec{c} = \hat{i} - 3\hat{j} - 5\hat{k} \), respectively form the vertices of a right angled triangle.▼
Solution:
\( \vec{AB} = \vec{b} - \vec{a} = -\hat{i} + 3\hat{j} + 5\hat{k} \). \( |\vec{AB}|^2 = 1+9+25 = 35 \).
\( \vec{BC} = \vec{c} - \vec{b} = -\hat{i} - 2\hat{j} - 6\hat{k} \). \( |\vec{BC}|^2 = 1+4+36 = 41 \).
\( \vec{CA} = \vec{a} - \vec{c} = 2\hat{i} - \hat{j} + \hat{k} \). \( |\vec{CA}|^2 = 4+1+1 = 6 \).
Here, \( |\vec{AB}|^2 + |\vec{CA}|^2 = 35 + 6 = 41 = |\vec{BC}|^2 \).
Since the sum of squares of two sides equals the square of the third side (Pythagoras theorem), they form a right-angled triangle.
Q18
In triangle ABC (Fig 10.18), which of the following is not true:▼
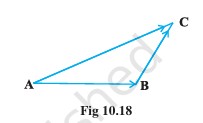
(A) \( \vec{AB} + \vec{BC} + \vec{CA} = \vec{0} \)
(B) \( \vec{AB} + \vec{BC} - \vec{AC} = \vec{0} \)
(C) \( \vec{AB} + \vec{BC} - \vec{AC} = \vec{0} \)
(D) \( \vec{AB} - \vec{CB} + \vec{CA} = \vec{0} \)
Solution:
By Triangle Law of Vector Addition: \( \vec{AB} + \vec{BC} = \vec{AC} \).
This implies \( \vec{AB} + \vec{BC} - \vec{AC} = \vec{0} \).
Also \( \vec{AC} = -\vec{CA} \), so \( \vec{AB} + \vec{BC} + \vec{CA} = \vec{0} \). This makes (A) true.
Checking (C): \( \vec{AB} + \vec{BC} - \vec{AC} = \vec{0} \) is true (Same as B).
Checking (D): \( \vec{AB} - \vec{CB} + \vec{CA} = \vec{AB} + \vec{BC} + \vec{CA} = \vec{0} \). True.
Answer: (C) is likely the intended answer if it was meant to be \( \dots + \vec{AC} = 0 \).
Q19
If \( \vec{a} \) and \( \vec{b} \) are two collinear vectors, then which of the following are incorrect:▼
(A) \( \vec{b} = \lambda \vec{a} \), for some scalar \( \lambda \)
(B) \( \vec{a} = \pm \vec{b} \)
(C) the respective components of \( \vec{a} \) and \( \vec{b} \) are not proportional
(D) both the vectors \( \vec{a} \) and \( \vec{b} \) have same direction, but different magnitudes.
Solution:
(A) True definition of collinearity.
(B) True for specific cases where \( \lambda = \pm 1 \), but as a general statement for *any* collinear vector, it's restrictive, but typically considered a valid *form* of collinearity relationship.
(C) Incorrect. For collinear vectors, components are proportional.
(D) Incorrect. Collinear vectors can have opposite directions.
Answer: (C) and (D) are incorrect statements. (D) is incorrect because directions can be opposite.
