Class 12-NCERT Solutions-Chapter-08-Application of Integrals

Solution:

The given equation of the ellipse \( \frac{x^2}{16} + \frac{y^2}{9} = 1 \), can be represented as:

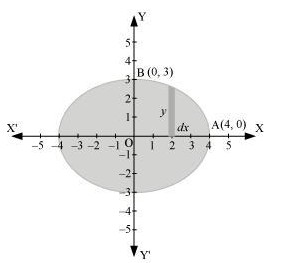
It can be observed that the ellipse is symmetrical about x-axis and y-axis.

Therefore, Area bounded by ellipse \( = 4 \times \text{Area of OAB} \)

\[ \begin{aligned} \text{Area of OAB} &= \int_{0}^{4} y \, dx \\ &= \int_{0}^{4} 3\sqrt{1 - \frac{x^2}{16}} \, dx \\ &= \frac{3}{4} \int_{0}^{4} \sqrt{16 - x^2} \, dx \\ &= \frac{3}{4} \left[ \frac{x}{2}\sqrt{16 - x^2} + \frac{16}{2}\sin^{-1}\frac{x}{4} \right]_{0}^{4} \\ &= \frac{3}{4} \left[ 2\sqrt{16 - 16} + 8\sin^{-1}(1) - 0 - 8\sin^{-1}(0) \right] \\ &= \frac{3}{4} \left[ 8\left(\frac{\pi}{2}\right) \right] \\ &= \frac{3}{4} [4\pi] \\ &= 3\pi \end{aligned} \]

Therefore, area bounded by the ellipse \( = 4 \times 3\pi = 12\pi \) square units.

Solution:

The given equation of the ellipse can be represented as:

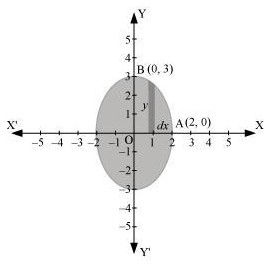
\[ \frac{x^2}{4} + \frac{y^2}{9} = 1 \Rightarrow y = 3\sqrt{1 - \frac{x^2}{4}} \quad \text{...(1)} \]

It can be observed that the ellipse is symmetrical about x-axis and y-axis.

Therefore, Area bounded by ellipse \( = 4 \times \text{Area of OAB} \)

\[ \begin{aligned} \text{Area of OAB} &= \int_{0}^{2} y \, dx \\ &= \int_{0}^{2} 3\sqrt{1 - \frac{x^2}{4}} \, dx \quad [\text{Using (1)}] \\ &= \frac{3}{2} \int_{0}^{2} \sqrt{4 - x^2} \, dx \\ &= \frac{3}{2} \left[ \frac{x}{2}\sqrt{4 - x^2} + \frac{4}{2}\sin^{-1}\frac{x}{2} \right]_{0}^{2} \\ &= \frac{3}{2} \left[ \frac{2}{2}\sqrt{4 - 4} + 2\sin^{-1}(1) - 0 \right] \\ &= \frac{3}{2} \left[ 2\left(\frac{\pi}{2}\right) \right] \\ &= \frac{3\pi}{2} \end{aligned} \]

Therefore, area bounded by the ellipse \( = 4 \times \frac{3\pi}{2} = 6\pi \) square units.

Solution:

The area bounded by the circle and the lines, \( x = 0 \) and \( x = 2 \), in the first quadrant is represented as:

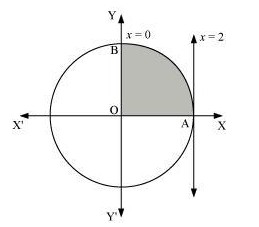
\[ \begin{aligned} \text{Area OAB} &= \int_{0}^{2} y \, dx \\ &= \int_{0}^{2} \sqrt{4 - x^2} \, dx \\ &= \left[ \frac{x}{2}\sqrt{4 - x^2} + \frac{4}{2}\sin^{-1}\frac{x}{2} \right]_{0}^{2} \\ &= 2\left(\frac{\pi}{2}\right) \\ &= \pi \text{ units} \end{aligned} \]

Thus, the correct answer is A.

Solution:

The area bounded by the curve, \( y^2 = 4x \), y-axis, and \( y = 3 \) is represented as:

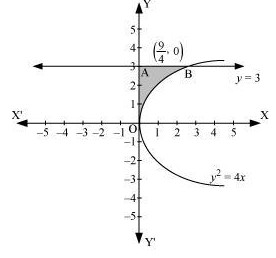
\[ \begin{aligned} \text{Area OAB} &= \int_{0}^{3} x \, dy \\ &= \int_{0}^{3} \frac{y^2}{4} \, dy \\ &= \frac{1}{4} \left[ \frac{y^3}{3} \right]_{0}^{3} \\ &= \frac{1}{12}(27) \\ &= \frac{9}{4} \text{ units} \end{aligned} \]

Thus, the correct answer is B.

Solution:

(i) The required area is represented by the shaded area ADCBA as:

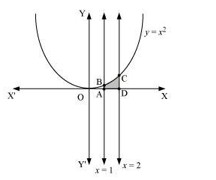
\[ \begin{aligned} \text{Area ADCBA} &= \int_{1}^{2} y \, dx \\ &= \int_{1}^{2} x^2 \, dx \\ &= \left[ \frac{x^3}{3} \right]_{1}^{2} \\ &= \frac{8}{3} - \frac{1}{3} \\ &= \frac{7}{3} \text{ units} \end{aligned} \]

(ii) The required area is represented by the shaded area ADCBA as:

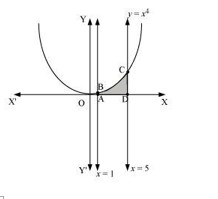
\[ \begin{aligned} \text{Area ADCBA} &= \int_{1}^{5} x^4 \, dx \\ &= \left[ \frac{x^5}{5} \right]_{1}^{5} \\ &= \frac{(5)^5}{5} - \frac{1}{5} \\ &= (5)^4 - \frac{1}{5} \\ &= 625 - \frac{1}{5} \\ &= 624.8 \text{ units} \end{aligned} \]

Solution:

The given equation is \( y = |x + 3| \).

The corresponding values of x and y are given in the following table:

On plotting these points, we obtain the graph of \( y = |x + 3| \) as follows:

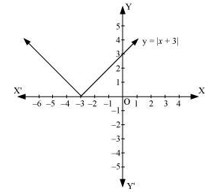
It is known that, \( (x + 3) \leq 0 \) for \( -6 \leq x \leq -3 \) and \( (x + 3) \geq 0 \) for \( -3 \leq x \leq 0 \).

\[ \begin{aligned} \text{Therefore, } \int_{-6}^{0} |x + 3| \, dx &= -\int_{-6}^{-3} (x + 3) \, dx + \int_{-3}^{0} (x + 3) \, dx \\ &= - \left[ \frac{x^2}{2} + 3x \right]_{-6}^{-3} + \left[ \frac{x^2}{2} + 3x \right]_{-3}^{0} \\ &= - \left[ \left(\frac{(-3)^2}{2} + 3(-3)\right) - \left(\frac{(-6)^2}{2} + 3(-6)\right) \right] + \left[ 0 - \left(\frac{(-3)^2}{2} + 3(-3)\right) \right] \\ &= - \left[ -\frac{9}{2} - \left(-\frac{9}{2}\right) \right] \\ &= 9 \end{aligned} \]

Solution:

The graph of \( y = \sin x \) can be drawn as:

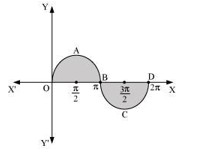
Therefore, Required area = Area OABO + Area BCDB

\[ \begin{aligned} &= \int_{0}^{\pi} \sin x \, dx + \left| \int_{\pi}^{2\pi} \sin x \, dx \right| \\ &= [-\cos x]_{0}^{\pi} + \left| [-\cos x]_{\pi}^{2\pi} \right| \\ &= [-\cos \pi + \cos 0] + |-\cos 2\pi + \cos \pi| \\ &= 1 + 1 + |(-1 - 1)| \\ &= 2 + |-2| \\ &= 2 + 2 = 4 \text{ units} \end{aligned} \]

Solution:

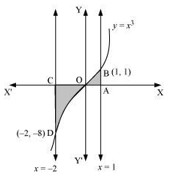
\[ \begin{aligned} \text{Required area} &= \int_{-2}^{1} y \, dx \\ &= \int_{-2}^{1} x^3 \, dx \\ &= \left[ \frac{x^4}{4} \right]_{-2}^{1} \\ &= \left[ \frac{1}{4} - \frac{(-2)^4}{4} \right] \\ &= \left( \frac{1}{4} - 4 \right) = -\frac{15}{4} \text{ units} \end{aligned} \]

As Area can not be negative, therefore, the area is 15/4.

Thus, the correct answer is B.

Solution:

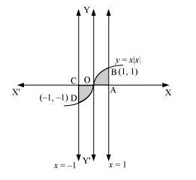
\[ \begin{aligned} \text{Required area} &= \int_{-1}^{1} y \, dx \\ &= \int_{-1}^{1} x|x| \, dx \\ &= \int_{-1}^{0} x^2 \, dx + \int_{0}^{1} x^2 \, dx \\ &= \left[ \frac{x^3}{3} \right]_{-1}^{0} + \left[ \frac{x^3}{3} \right]_{0}^{1} \\ &= -\left( -\frac{1}{3} \right) + \frac{1}{3} \\ &= \frac{2}{3} \text{ units} \end{aligned} \]

Thus, the correct answer is C.